题目内容
5. 函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b2-4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b-1)x+c<0;其中正确的个数有2个.
函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b2-4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b-1)x+c<0;其中正确的个数有2个.
分析 由函数y=x2+bx+c与x轴无交点,可得b2-4c<0;当x=1时,y=1+b+c=1;当x=3时,y=9+3b+c=3;当1<x<3时,二次函数值小于一次函数值,可得x2+bx+c<x,继而可求得答案.
解答 解:∵函数y=x2+bx+c与x轴无交点,
∴b2-4ac<0;
故①错误;
当x=1时,y=1+b+c=1,
故②错误;
∵当x=3时,y=9+3b+c=3,
∴3b+c+6=0;
③正确;
∵当1<x<3时,二次函数值小于一次函数值,
∴x2+bx+c<x,
∴x2+(b-1)x+c<0.
故④正确.
故答案是:2.
点评 主要考查图象与二次函数系数之间的关系.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
13.下列各组数中,不可能是一个三角形三边长的是( )
| A. | 5,7,12 | B. | 5,7,7 | C. | 5,12,13 | D. | 5,7,11 |
14.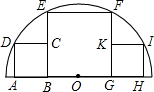 如图,三个相邻的正方形内接于半圆,若小正方形的面积为16cm2,则正方形BEFG的边长为( )
如图,三个相邻的正方形内接于半圆,若小正方形的面积为16cm2,则正方形BEFG的边长为( )
 如图,三个相邻的正方形内接于半圆,若小正方形的面积为16cm2,则正方形BEFG的边长为( )
如图,三个相邻的正方形内接于半圆,若小正方形的面积为16cm2,则正方形BEFG的边长为( )| A. | 4cm | B. | 8cm | C. | 4$\sqrt{5}$cm | D. | 6$\sqrt{2}$cm |