题目内容
6.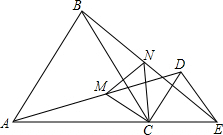 如图,△ABC、△DEC均为等边三角形,点M为线段AD的中点,点N为线段BE的中点,求证:△CNM为等边三角形.
如图,△ABC、△DEC均为等边三角形,点M为线段AD的中点,点N为线段BE的中点,求证:△CNM为等边三角形.
分析 先根据等边三角形的性质求出AC=BC,CD=CE,∠ACB=∠DCE=60°,再由SAS定理得出△ACD≌△BCE,根据点M为线段AD的中点,点N为线段BE的中点得出MC=NC,故∠ACM=∠BCN,所以∠ACB=∠MCB+∠ACM=∠MCB+∠BCN=∠MCN=60°,再由MC=NC即可得出结论.
解答 证明:△ABC,△DEC均为等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°.
∴∠ACB+∠BCD=∠DCE+∠BCD.
在△ACD与△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS).
∴∠DAC=∠CBE,AD=BE,
又∵点M为线段AD的中点,点N为线段BE的中点,
∴AM=BN,
在△ACM与△BCN中,
$\left\{\begin{array}{l}{AC=BC}\\{∠CAM=∠CBN}\\{AM=BN}\end{array}\right.$,
∴△ACM≌△BCN(SAS).
∴MC=NC
∴∠ACM=∠BCN,
∴∠ACB=∠MCB+∠ACM=∠MCB+∠BCN=∠MCN=60°.
∵MC=NC,
∴△CNM为等边三角形.
点评 本题考查的是全等三角形的判定与性质,熟知判定全等三角形的SSS,SAS及AAS定理是解答此题的关键.

练习册系列答案
相关题目
14.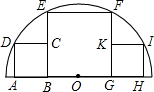 如图,三个相邻的正方形内接于半圆,若小正方形的面积为16cm2,则正方形BEFG的边长为( )
如图,三个相邻的正方形内接于半圆,若小正方形的面积为16cm2,则正方形BEFG的边长为( )
 如图,三个相邻的正方形内接于半圆,若小正方形的面积为16cm2,则正方形BEFG的边长为( )
如图,三个相邻的正方形内接于半圆,若小正方形的面积为16cm2,则正方形BEFG的边长为( )| A. | 4cm | B. | 8cm | C. | 4$\sqrt{5}$cm | D. | 6$\sqrt{2}$cm |
1.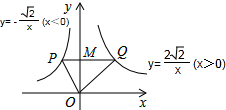 函数y=-$\frac{\sqrt{2}}{x}$(x<0)和y=$\frac{2\sqrt{2}}{x}$(x>0)的图象如图所示,O为坐标原点,M是y轴正半轴上任意一点,过点M作PQ∥x轴,分别与图中的函数图象相交于P、Q两点,连接OP、OQ,则△OPQ的面积为( )
函数y=-$\frac{\sqrt{2}}{x}$(x<0)和y=$\frac{2\sqrt{2}}{x}$(x>0)的图象如图所示,O为坐标原点,M是y轴正半轴上任意一点,过点M作PQ∥x轴,分别与图中的函数图象相交于P、Q两点,连接OP、OQ,则△OPQ的面积为( )
 函数y=-$\frac{\sqrt{2}}{x}$(x<0)和y=$\frac{2\sqrt{2}}{x}$(x>0)的图象如图所示,O为坐标原点,M是y轴正半轴上任意一点,过点M作PQ∥x轴,分别与图中的函数图象相交于P、Q两点,连接OP、OQ,则△OPQ的面积为( )
函数y=-$\frac{\sqrt{2}}{x}$(x<0)和y=$\frac{2\sqrt{2}}{x}$(x>0)的图象如图所示,O为坐标原点,M是y轴正半轴上任意一点,过点M作PQ∥x轴,分别与图中的函数图象相交于P、Q两点,连接OP、OQ,则△OPQ的面积为( )| A. | $\sqrt{2}$ | B. | $\frac{3}{2}\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | $\frac{5}{2}\sqrt{2}$ |
18.甲、乙两人5次射击命中的环数如下:
则这两人5次射击命中的环数的平均数$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$=8,方差S甲2( )S乙2.
| 甲 | 7 | 9 | 8 | 6 | 10 |
| 乙 | 7 | 8 | 9 | 8 | 8 |
| A. | > | B. | < | C. | = | D. | 以上都不对 |
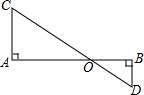 如图,AB与CD交于O点,已知AC⊥AB,BD⊥AB,AO=50cm,BO=25cm,CD=150cm,求CO和DO.
如图,AB与CD交于O点,已知AC⊥AB,BD⊥AB,AO=50cm,BO=25cm,CD=150cm,求CO和DO.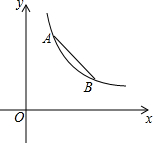 已知反比例函数y=$\frac{k}{x}$的图象经过A(m,m+1),B(m+3,m-1)两点,C为x轴上一点,D为y轴上一点,以点A、B、C、D为顶点的四边形是平行四边形,求直线CD的解析式.
已知反比例函数y=$\frac{k}{x}$的图象经过A(m,m+1),B(m+3,m-1)两点,C为x轴上一点,D为y轴上一点,以点A、B、C、D为顶点的四边形是平行四边形,求直线CD的解析式.