Question

如图，已知：点E在△ABC的边AB上，∠C=90°，以AE为直径的⊙O切BC于D．
（1）求证：AD平分∠BAC．
（2）已知∠B=30°，AD=2

3

，求图中阴影部分的面积．

Answer 1

考点：切线的性质,扇形面积的计算

专题：

分析：（1）连接OD，可证明OD∥AC，结合平行线的性质可证得结论；
（2）由直角三角形的性质可求得BD，再结合三角函数可求得OD，可求得△OBD和扇形OED的面积，可求得阴影部分面积．

解答：（1）证明：如图，连接OD，

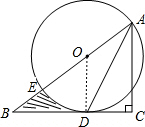
∵BC为⊙O的切线，
∴OD⊥BC，且∠C=90°，
∴OD∥AC，
∴∠ODA=∠DAC，
又∵OD=OA，
∴∠OAD=∠ODA，
∴∠OAD=∠DAC，
即AD平分∠BAC；
（2）解：∵∠B=30°，
∴∠BAC=60°，
∴∠BAD=∠DAC=30°，
∴BD=AD=2

3

，
在Rt△OBD中，tan∠B=

OD

BD

，即

3

3

=

OD

2 3

，
∴OD=2，且∠BOD=60°，
∴S_阴影=S_△OBD-S_扇形OED=

1

2

BD•OD-

60πOD2

360

=

1

2

×2

3

×2-

4π

6

=2

3

-

2π

3

．

点评：本题主要考查切线的性质，掌握过切点的半径和切线垂直是解题的关键，注意扇形面积公式的应用．