题目内容
15.已知不等式组$\left\{\begin{array}{l}{2x-3≥1}\\{\frac{2x-5a}{3}-x>2}\end{array}\right.$只有3个正整数解,则a的取值范围是-$\frac{11}{5}$≤a<-2.分析 首先解不等式组,根据不等式组只有三个正整数解,即可确定a的范围.
解答 解:$\left\{\begin{array}{l}{2x-3≥1①}\\{\frac{2x-5a}{3}-x>2②}\end{array}\right.$
解不等式①得,x≥2,
解不等式②得,x<-5a-6.
则不等式组的解集是:2≤x<-5a-6,
则正整数解是2,3,4;
则4<-5a-6≤5,
解得-$\frac{11}{5}$≤a<-2.
故答案是:-$\frac{11}{5}$≤a<-2.
点评 本题考查不等式组的解法及整数解的确定.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
相关题目
20.在同一直角坐标平面内,如果y=k1x与$y=\frac{k_2}{x}$没有交点,那么k1和k2的关系一定是( )
| A. | k1<0,k2>0 | B. | k1>0,k2<0 | C. | k1、k2同号 | D. | k1、k2异号 |
 在△ABC中,∠ACB=90°,CD⊥AB于D,AE是∠CAB的平分线,且交CD于E,CB于F,求证:AF:AE=CB:CD.
在△ABC中,∠ACB=90°,CD⊥AB于D,AE是∠CAB的平分线,且交CD于E,CB于F,求证:AF:AE=CB:CD.
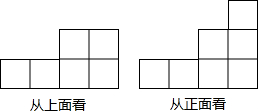 由一些大小相同的小正方体组成的简单几何体从正面和上面看到的平面图形如图所示.
由一些大小相同的小正方体组成的简单几何体从正面和上面看到的平面图形如图所示.