题目内容
如图，平行四边形ABCD中，EF过对角线的交点O，AB＝4，AD＝3，OF＝1.3，则四边形BCEF的周长为（ ）
A. 8.3 B. 9.6 C. 12.6 D. 13.6
B
【解析】【解析】
根据平行四边形的中心对称性得：OF=OE=1.3．∵?ABCD的周长=（4+3）×2=14
∴四边形BCEF的周长=×?ABCD的周长+2.6=9.6．故选B．
英才点津系列答案
红果子三级测试卷系列答案
课堂练加测系列答案如图，点A，B的坐标分别为（1， 4）和（4， 4），抛物线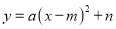
的顶点在线段AB上运动，与x轴交于C、D两点（C在D的左侧），点C的横坐标最小值为-3，则点D的横坐标最大值为_______。
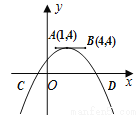
8
【解析】当抛物线y=a（x-m）2+n的顶点在线段AB的A点上时，点C的横坐标最小，把A（1，4）代入得：y=a（x-1）2+4，把C（-3，0）代入得：0=a（-3-1）2+4，解得：a=-，即：y=-（x-1）2+4，再根据题意知抛物线y=a（x-m）2+n的顶点在线段AB上运动，可得抛物线的a永远等于-，当抛物线的顶点运动到B时，D的横坐标最大，把a=-和B（4，4）代入y=a（x... 已知2a－3x＋1＝0，3b－2x－16＝0，且a≤4＜b，求x的取值范围．
【解析】【解析】
由已知得：a＝，b＝
又∵a≤4＜b
∴
解此不等式组，得
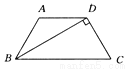
－2＜x≤3. 如图所示，在梯形ABCD中．AD∥BC，AB＝DC，BD⊥DC于点D，且∠C＝60°．若AD＝5㎝．则梯形的腰长为________㎝．
5
【解析】【解析】
∵BD⊥DC于D，且∠C=60°，∴∠DBC=30°．∵AD∥BC，AB=DC，∴∠ABC=∠C=60°，∴∠ADB=∠DBC=∠ABD=30°，∴AB=AD=5cm．故答案为：5． 已知□ABCD中，∠B=70°，则∠A=______，∠C=______，∠D=______.
110° 110° 70°
【解析】【解析】
由平行四边形的性质得：∠A=180°-∠B=110°，∠C=∠A=70°，∠D=180°-∠B=110°．
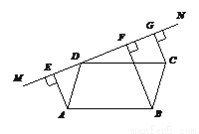
故答案为：110°，110°，70°． 如图，直线MN过□ABCD的顶点D，过A，B，C三点，分别作MN的垂线，垂足分别是E，F，G．
求证：DE＝FG．
答案见解析
【解析】试题分析：作CH⊥BF与H．可证△AED≌△BHC，得到ED=HC，再由平行线间的距离处处相等得到FG=CH，即可得到结论．
试题解析：证明：作CH⊥BF与H．
∵AE⊥MN，BF⊥MN，∴AE∥BF，∴∠EAD+∠DAB+∠ABF=180°．
∵ABCD是平行四边形，∴AD∥BC，AD=BC，∴∠DAB+∠ABF+∠HBC=180°，∴∠EAD=∠HB... 如图所示，已知D，E，F分别在△ABC的边BC，AB，AC上，且DE∥AF，DE＝AF，将FD延长至G，使FG＝2DF，连接AG，则ED，AG互相平分吗?请说明理由．
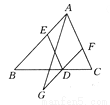
互相平分
【解析】试题分析：求ED与AG互相平分，只要证明四边形AEGD是平行四边形即可解答，由DE∥AC，DE=AF，可得四边形AEDF是平行四边形，所以，AE∥DF且AE=DF，又FG=2DF，则AE=GD，所以，四边形AEGD是平行四边形，即可得出ED与AG互相平分．
试题解析：证明：如图，连接AD，GE，∵DE∥AC，DE=AF，∴四边形AEDF是平行四边形，∴AE∥DF且AE... 倡导健康生活，推进全民健身，某社区要购进A、B两种型号的健身器材若干套，A、B两种型号健身器材的购买单价分别为每套310元，460元，且每种型号健身器材必须整套购买．
(1)若购买A、B两种型号的健身器材共50套，且恰好支出20000元，求A、B两种型号健身器材各购买多少套？
(2)若购买A、B两种型号的健身器材共50套，且支出不超过18000元，求A种型号健身器材至少要购买多少套？
（1）购买A种型号健身器材20套，B型器材健身器材30套； （2）A种型号健身器材至少要购买34套．
【解析】试题分析：（1）设购买A种型号健身器材x套，B型器材健身器材y套，根据题目中的“A，B两种型号的健身器材共50套、共支出20000元”可列方程组，解方程组即可；（2）设购买A型号健身器材m套，根据“A型器材总费用+B型器材总费用≤18000”，列不等式求解即可．
试题解析：（1... 下列命题中，其逆命题为真命题的是（ ）
A. 若a＝b，则a2＝b2 B. 同位角相等
C. 两边和一角对应相等的两个三角形全等 D. 等腰三角形两底角不相等
C
【解析】根据互为逆命题的关系，题设和结论互换，可知：
若a=b，则a2＝b2的逆命题为：若a2＝b2，则a=b，是假命题；
同位角相等的逆命题为：相等的角是同位角，是假命题；
两边和一角对应相等的两个三角形全等的逆命题是：全等三角形的对应边相等，对应角相等，是真命题；
等腰三角形的两底角不相等的逆命题为：两个角不相等的三角形是等腰三角形，是假命题.
故选：C...