题目内容
12.已知:△ABC是⊙O的内接三角形,AB=AC,在∠BAC所对弧AC上,任取一点D,连接AD,BD,CD.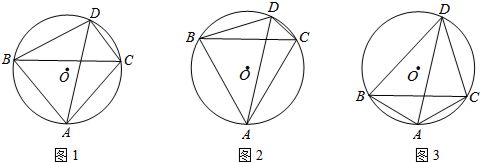
(1)如图1,∠BAC=α,直接写出∠ADB的大小(用含α的式子表示);
(2)如图2,如果∠BAC=60°,求证:BD+CD=AD;
(3)如图3,如果∠BAC=120°,那么BD+CD与AD之间的数量关系是什么?写出猜测并加以证明;
(4)如果∠BAC=α,直接写出BD+CD与AD之间的数量关系.
分析 (1)利用AB=AC得到$\widehat{AB}$=$\widehat{AC}$,根据圆周角定理得∠ADB=∠ADC,再利用圆内接四边形的性质得到∠BAC+∠BDC=180°,所以∠ADB=$\frac{1}{2}$(180°-α)=90°-$\frac{1}{2}$α;
(2)延长BD到E,使得DE=DC,如图2,先证明△ABC是等边三角形得到BC=AC,∠BAC=∠ACB=60°,再证明△DCE是等边三角形得到DC=CE,∠DCE=60°,于是得到∠ACD=∠BCE,则可证明△ACD≌△BCE得到BE=AD,于是易得AD=BD+CD;
(3)延长DB到E,使得BE=DC,连接AE,过点A作AF⊥BD于点F,如图3,有(1)的结论得到∠1=∠2=90°-$\frac{1}{2}$×120°=30°,在Rt△ADF中,利用余弦定义得到DF=ADcos30°=$\frac{\sqrt{3}}{2}$AD,再证明△EBA≌△DCA得到∠2=∠1,则∠E=∠1,则可判断△ADE为等腰三角形,所以DF=EF,易得DE=BD+CD=2DF,于是有BD+CD=$\sqrt{3}$AD;
(4)与(3)的证明方法一样,如图3,只是∠1=90°-$\frac{1}{2}$α,在Rt△ADF中DF=ADcos(90°-$\frac{1}{2}$α),然后利用DE=BD+CD=2DF得到BD+CD=2ADcos(90°-$\frac{1}{2}$α).
解答 (1)解:∵AB=AC,
∴$\widehat{AB}$=$\widehat{AC}$,
∴∠ADB=∠ADC,
∵∠BAC+∠BDC=180°,
∴∠BDC=180°-α,
∴∠ADB=$\frac{1}{2}$(180°-α)=90°-$\frac{1}{2}$α;
(2)证明:延长BD到E,使得DE=DC,如图2,
∵∠BAC=60°,AB=AC
∴△ABC是等边三角形,
∴BC=AC,∠BAC=∠ACB=60°,
∵∠EDC=∠BAC=60°,
∵DC=DE,
∴△DCE是等边三角形,
∴DC=CE,∠DCE=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{∠CAD=∠CBE}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE,
∴BE=AD,
∵BE=BD+DE,
∴AD=BD+CD;
(3)解:BD+CD=$\sqrt{3}$AD.理由如下:
延长DB到E,使得BE=DC,连接AE,过点A作AF⊥BD于点F,如图3,
∵AB=AC,
∴$\widehat{AB}$=$\widehat{AC}$,
∴∠1=∠2=90°-$\frac{1}{2}$×120°=30°,
在Rt△ADF中,∵cos∠1=$\frac{DF}{AD}$,
∴DF=ADcos30°=$\frac{\sqrt{3}}{2}$AD,
在△EBA和△DCA中,
$\left\{\begin{array}{l}{BE=CD}\\{∠EBA=∠DCA}\\{BA=CA}\end{array}\right.$,
∴△EBA≌△DCA,
∴∠2=∠1,
∴∠E=∠1,
∴AE=AD,
∴DF=EF,
∴DE=BD+CD=2DF,
∴BD+CD=2×$\frac{\sqrt{3}}{2}$AD=$\sqrt{3}$AD;
(4)与(3)的证明方法一样,如图3,∠1=∠2=90°-$\frac{1}{2}$α,
在Rt△ADF中,∵cos∠1=$\frac{DF}{AD}$,
∴DF=ADcos(90°-$\frac{1}{2}$α),
而DE=BD+CD=2DF,
∴BD+CD=2ADcos(90°-$\frac{1}{2}$α).
点评 本题考查了圆的综合题:熟练掌握圆周角定理、等腰三角形的性质和等边三角形的性质;会利用三角形全等解决线段相等的问题;学会把两线段的和化为一条线段.

| A. | x<5 | B. | x>5 | C. | x≥5 | D. | x≤5 |
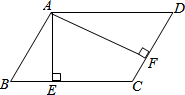 已知?ABCD的周长为36cm,过点A作AE⊥BC,AF⊥CD,若AE=2cm,AF=4cm,求平行四边形各边的长.
已知?ABCD的周长为36cm,过点A作AE⊥BC,AF⊥CD,若AE=2cm,AF=4cm,求平行四边形各边的长.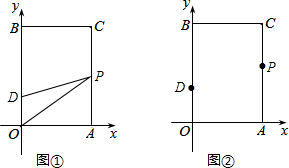
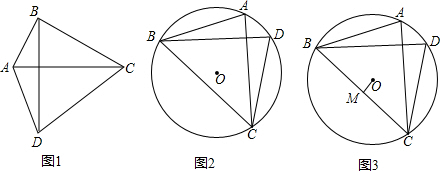
 如图,两条平行线AB、CD被直线BC所截,一组同旁内角的平分线相交于点E,则∠BEC的度数是90°.
如图,两条平行线AB、CD被直线BC所截,一组同旁内角的平分线相交于点E,则∠BEC的度数是90°. 如图,AB是⊙O的直径,C,D两点在⊙O上,∠BCD=25°,则∠AOD的度数为130°.
如图,AB是⊙O的直径,C,D两点在⊙O上,∠BCD=25°,则∠AOD的度数为130°.