题目内容
6.设m是方程x2-3x+1=0的一个实数根,则$\frac{{{m^4}+{m^2}+1}}{m^2}$=8.分析 利用一元二次方程的解的意义得到m2-3m+1=0,两边除以m得到m+$\frac{1}{m}$=3,再把原式变形得到原式=m2+1+$\frac{1}{{m}^{2}}$=(m+$\frac{1}{m}$)2-2+1,然后利用整体代入的方法计算.
解答 解:∵m是方程x2-3x+1=0的一个实数根,
∴m2-3m+1=0,
∴m+$\frac{1}{m}$=3,
∴原式=m2+1+$\frac{1}{{m}^{2}}$
=(m+$\frac{1}{m}$)2-2+1
=9-2+1
=8.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.

练习册系列答案
相关题目
11.已知双曲线y=$\frac{k}{x}$(k≠0)上有一点P(m,n),m,n是关于t的一元二次方程t2-3t+k=0的两根,且P点到原点的距离为$\sqrt{13}$,则双曲线的表达式为( )
| A. | y=$\frac{2}{x}$ | B. | y=-$\frac{2}{x}$ | C. | y=$\frac{4}{x}$ | D. | y=-$\frac{4}{x}$ |

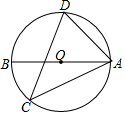 如图,AB为⊙O直径,CD为⊙O的弦,∠ACD=43°,∠BAD的度数为47°.
如图,AB为⊙O直径,CD为⊙O的弦,∠ACD=43°,∠BAD的度数为47°.