题目内容
16.已知a、b为有理数,且8-(a+b)=0,则a+b的立方根是2$\sqrt{2}$.分析 先依据等式求得a+b的值,最后利用立方根的定义求解即可.
解答 解:∵8-(a+b)=0,
∴a+b=8.
∴a+b的立方根=$\root{3}{8}$=2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题主要考查的是立方根的定义,熟练掌握求得a+b的值是解题的关键.

练习册系列答案
相关题目
9.下列说法中,错误的是( )
| A. | -t2的系数是-1 | B. | -$\frac{2mn}{3}$的系数是-$\frac{2}{3}$ | ||
| C. | xy2的系数是1 | D. | 3πa2的系数是3 |
1.下列与:-9+31+28-45相等的是( )
| A. | -9+45+28-31 | B. | 31-45-9+28 | C. | 28-9-31-45 | D. | 45-9-28+31 |
8.已知(m+2)x|m|-1-6=0是关于x的一元一次方程,则m的值是( )
| A. | 1 | B. | -1 | C. | -2 | D. | 2 |
5.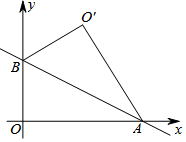 如图,直线y=-$\frac{{\sqrt{3}}}{3}$x+2与x轴,y轴分别交于A,B两点,把△AOB沿着直线AB翻折后得到△AO'B,则点O'的坐标是( )
如图,直线y=-$\frac{{\sqrt{3}}}{3}$x+2与x轴,y轴分别交于A,B两点,把△AOB沿着直线AB翻折后得到△AO'B,则点O'的坐标是( )
 如图,直线y=-$\frac{{\sqrt{3}}}{3}$x+2与x轴,y轴分别交于A,B两点,把△AOB沿着直线AB翻折后得到△AO'B,则点O'的坐标是( )
如图,直线y=-$\frac{{\sqrt{3}}}{3}$x+2与x轴,y轴分别交于A,B两点,把△AOB沿着直线AB翻折后得到△AO'B,则点O'的坐标是( )| A. | $({\sqrt{3}\;,\;\;3})$ | B. | $({3\;,\;\;\sqrt{3}})$ | C. | $({2\;,\;\;2\sqrt{3}})$ | D. | $({2\sqrt{3}\;,\;\;4})$ |

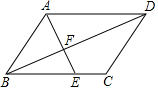 如图,在?ABCD中,E是BC上一点,AE交BD于F,BE=3,EC=2,S△AFD=10,则S△BEF=$\frac{18}{5}$.
如图,在?ABCD中,E是BC上一点,AE交BD于F,BE=3,EC=2,S△AFD=10,则S△BEF=$\frac{18}{5}$.