题目内容
17．求出下列图中直角三角形中未知边的长度．
分析 分别根据勾股定理求解即可．
解答 解：图1中，c=$\sqrt{{5}^{2}+1{2}^{2}}$=13；
图2中，b=$\sqrt{1{0}^{2}-{6}^{2}}$=8；
图3中，∵大直角三角形的直角边=$\sqrt{2{6}^{2}-2{4}^{2}}$=10，
∴h=$\sqrt{1{0}^{2}-{6}^{2}}$=8．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
智慧小复习系列答案
相关题目
8．已知（m+2）x|m|-1-6=0是关于x的一元一次方程，则m的值是（ ）
| A． | 1 | B． | -1 | C． | -2 | D． | 2 |
5．
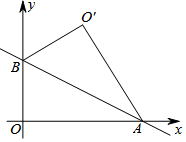如图，直线y=-$\frac{{\sqrt{3}}}{3}$x+2与x轴，y轴分别交于A，B两点，把△AOB沿着直线AB翻折后得到△AO'B，则点O'的坐标是（ ）
如图，直线y=-$\frac{{\sqrt{3}}}{3}$x+2与x轴，y轴分别交于A，B两点，把△AOB沿着直线AB翻折后得到△AO'B，则点O'的坐标是（ ）| A． | $（{\sqrt{3}\;，\;\;3}）$ | B． | $（{3\;，\;\;\sqrt{3}}）$ | C． | $（{2\;，\;\;2\sqrt{3}}）$ | D． | $（{2\sqrt{3}\;，\;\;4}）$ |
如图，∠A+∠B+∠C+∠D+∠E+∠F=360°．