Question

如图，△ABC以AB为直径，中点O为圆心作圆交BC于P，使BP=CP，作PE⊥AC，求证：PE为切线．（用两种方法）

Answer 1

考点：切线的判定

专题：证明题

分析：方法一：连接OP，得出OP是△ABC的中位线，进而利用平行线的性质得出∠OPE=90°，即可得出答案；
方法二：连接AP，得出∠OPA=∠PAE，进而得出∠PAE+∠APE=90°，即可得出∠OPA+∠APE=90°，得出答案即可．

解答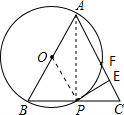：方法一：
证明：连接OP，
∵O为AB的中点，BP=PC，
∴OP是△ABC的中位线，
∴OP∥AC，
∵∠PEC=90°，
∴∠OPE=90°，
∴PE为⊙O切线；

方法二：
证明：连接AP，
∵AB是⊙O的直径，
∴∠APB=90°，
∵BP=PC，
∴AB=AC，∠BAP=∠CAP，
∵∠BAP=∠OPA，
∴∠OPA=∠PAE，
∵∠AEP=90°，
∴∠PAE+∠APE=90°，
∴∠OPA+∠APE=90°，
∴PE为⊙O切线．

点评：此题主要考查了切线的判定以及等腰三角形的性质等知识，熟练应用切线的判定方法是解题关键．