题目内容
等边三角形的内切圆半径与外接圆半径分别是r、R,则
的值是 .
| R |
| r |
考点:三角形的内切圆与内心,三角形的外接圆与外心
专题:
分析:作出辅助线OD、OE,证明△AOD为直角三角形且∠OAD为30°,即可求出OD、OA的比.
解答: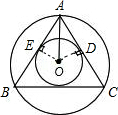 解:如图,连接OD、OE;
解:如图,连接OD、OE;
因为AB、AC切圆O与E、D,
所以OE⊥AB,OD⊥AC,
又因为AO=AO,
EO=DO,
所以△AEO≌△ADO(HL),
故∠DAO=∠EAO;
又∵△ABC为等边三角形,
∴∠BAC=60°,
∴∠OAC=60°×
=30°,
∴OD:AO=1:2.
等边三角形的内切圆半径与外接圆半径的比是
.
故答案是:
.
 解:如图,连接OD、OE;
解:如图,连接OD、OE;因为AB、AC切圆O与E、D,
所以OE⊥AB,OD⊥AC,
又因为AO=AO,
EO=DO,
所以△AEO≌△ADO(HL),
故∠DAO=∠EAO;
又∵△ABC为等边三角形,
∴∠BAC=60°,
∴∠OAC=60°×
| 1 |
| 2 |
∴OD:AO=1:2.
等边三角形的内切圆半径与外接圆半径的比是
| 1 |
| 2 |
故答案是:
| 1 |
| 2 |
点评:此题将等边三角形的内切圆半径和外接圆半径综合考查,找到直角三角形,将三角形内切圆和三角形外接圆联系起来是解题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
下列线段能构成比例线段的是( )
| A、1,2,3,4 | ||||||
B、1,
| ||||||
C、
| ||||||
| D、2,5,3,4 |
某小组10个女生做仰卧起坐,仰卧起坐次数的测试数据如下表,则这组数据的平均数和中位数分别是( )
| 次数 | 35 | 38 | 40 | 41 | 42 |
| 人数 | 1 | 1 | 3 | 3 | 2 |
| A、38.8和40 |
| B、40和40 |
| C、40和40.5 |
| D、38.8和40.5 |
 如图,△ABC以AB为直径,中点O为圆心作圆交BC于P,使BP=CP,作PE⊥AC,求证:PE为切线.(用两种方法)
如图,△ABC以AB为直径,中点O为圆心作圆交BC于P,使BP=CP,作PE⊥AC,求证:PE为切线.(用两种方法) 如图,路灯距地面8米,一身高1.6米的人沿穿过灯下的直路以84米/分的速度行走,求该人1分钟从A到B时,人影的长度变化了多少米?
如图,路灯距地面8米,一身高1.6米的人沿穿过灯下的直路以84米/分的速度行走,求该人1分钟从A到B时,人影的长度变化了多少米?