题目内容
4. 如图,已知直线AB∥CD,∠C=105°,∠A=45°,那么∠E的值为( )
如图,已知直线AB∥CD,∠C=105°,∠A=45°,那么∠E的值为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
分析 设AB与CE相交于点F,先根据平行线的性质得出∠BFE的度数,再由三角形外角的性质即可得出结论.
解答  解:设AB与CE相交于点F,
解:设AB与CE相交于点F,
∵直线AB∥CD,∠C=105°,
∴∠BFE=∠C=105°.
∵∠A=45°,
∴∠E=∠BFE-∠A=105°-45°=60°.
故选B.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.

练习册系列答案
相关题目
13.已知二次函数y=-x2+2x+1的顶点为A,与y轴交点为B,动点P(x,0)在x轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
| A. | (-1,0) | B. | (1,0) | C. | (-$\frac{1}{3}$,0) | D. | ($\frac{1}{3}$,0) |
8. 如图是由5个形状、大小完全相同的正六边形组成的图案,我们把正六边形的顶点称为格点.若Rt△ABC的顶点都在格点上,且AB为Rt△ABC的斜边,则Rt△ABC的个数有( )
如图是由5个形状、大小完全相同的正六边形组成的图案,我们把正六边形的顶点称为格点.若Rt△ABC的顶点都在格点上,且AB为Rt△ABC的斜边,则Rt△ABC的个数有( )
 如图是由5个形状、大小完全相同的正六边形组成的图案,我们把正六边形的顶点称为格点.若Rt△ABC的顶点都在格点上,且AB为Rt△ABC的斜边,则Rt△ABC的个数有( )
如图是由5个形状、大小完全相同的正六边形组成的图案,我们把正六边形的顶点称为格点.若Rt△ABC的顶点都在格点上,且AB为Rt△ABC的斜边,则Rt△ABC的个数有( )| A. | 2个 | B. | 4个 | C. | 6个 | D. | 8个 |
11.下列二次根式:$\sqrt{5},\sqrt{\frac{1}{3}},\sqrt{0.5a},-2\sqrt{{a^2}b},\sqrt{{x^2}+{y^2}}$中,是最简二次根式的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
12.正方形和下列边长相同的正多边形地砖组合中,不能够铺满地面的是( )
| A. | 正三角形 | B. | 正六边形 | ||
| C. | 正八边形 | D. | 正三角形和正六边形 |
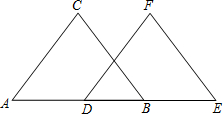 看图填空:已知:如图,BC∥EF,AD=BE,BC=EF,试说明△ABC≌△DEF
看图填空:已知:如图,BC∥EF,AD=BE,BC=EF,试说明△ABC≌△DEF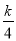 =0有两个不相等的实数根,则k的取值范围是__________.
=0有两个不相等的实数根,则k的取值范围是__________.