题目内容
18．已知一个三角形各边的比为2：3：4，联结各边中点所得的三角形的周长为18cm，那么原三角形最短的边的长为8cm．分析 由中点和中位线定义可得新三角形的各边长为原三角形各边长的一半，即可求各边长．
解答 解：由题意，设三边分别为2xcm，3xcm，4xcm，
则各边中点所得的三角形的边长分别为xcm，1.5xcm，2xcm
则x+1.5x+2x=18，
解得x=4，
∴2x=8cm
原三角形最短的边的长为8cm；
故答案为：8．
点评 本题考查了三角形中位线定理．解决本题的关键是利用中点定义和中位线定理得到新三角形各边长与原三角形各边长的数量关系．
练习册系列答案
华东师大版一课一练系列答案
孟建平名校考卷系列答案
相关题目
如图，在正方形ABCD中，△APBC是等边三角形，连接PD，DB，则$\frac{{S}_{△BPD}}{{S}_{正方形ABCD}}$=$\frac{\sqrt{3}-1}{4}$．
13．
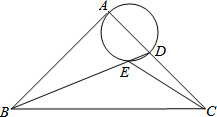如图，在等腰直角△ABC中，∠BAC=90°，AB=AC，BC=4$\sqrt{2}$，点D是AC上一动点，连接BD，以AD为直径的圆交BD于点E，则线段CE长度的最小值是（ ）
如图，在等腰直角△ABC中，∠BAC=90°，AB=AC，BC=4$\sqrt{2}$，点D是AC上一动点，连接BD，以AD为直径的圆交BD于点E，则线段CE长度的最小值是（ ）| A． | 2 | B． | 4 | C． | $2\sqrt{2}-2$ | D． | $2\sqrt{5}-2$ |
如图，在平面直角坐标系xOy中，抛物线y=$\frac{1}{4}$x2+bx+c经过点A（-2，0）和原点，点B在抛物线上且tan∠BAO=$\frac{1}{2}$，抛物线的对称轴与x轴相交于点P．
如图：证明：∠A+∠B+∠C=180°．
如图，在△ABC中，AC=BC，∠ACB=90°，点D在BC的延长线上，连接AD，过B作BE⊥AD，垂足为E，交AC于点F，连接CE．