题目内容
19.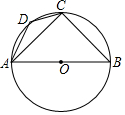 如图所示,AB是⊙O的直径,点C、D在⊙O上,若∠DAC=20°,∠B=50°,试求∠BCD的度数.
如图所示,AB是⊙O的直径,点C、D在⊙O上,若∠DAC=20°,∠B=50°,试求∠BCD的度数.
分析 由AB是⊙O的直径,得到∠ACB=90°,根据三角形的内角和得到∠CAB=40°,根据圆内接四边形的性质即可得到结论.
解答 解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠B=50°,
∴∠CAB=40°,
∵∠DAC=20°,
∴∠DAB=60°,
∴∠BCD=180°-60°=120°.
点评 此题考查了圆周角定理以及圆的内接四边形的性质.熟练掌握圆周角定理解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7. 如图,在?ABCD中,下列结论错误的是( )
如图,在?ABCD中,下列结论错误的是( )
 如图,在?ABCD中,下列结论错误的是( )
如图,在?ABCD中,下列结论错误的是( )| A. | ∠1=∠2 | B. | ∠1=∠3 | C. | AB=CD | D. | ∠BAD=∠BCD |
14.若两个相似三角形的周长之比为2:3,则它们对应边的比为( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{2}$ |
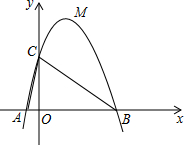 如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1
如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1

