题目内容
9.已知点A在数轴上对应的数为a,点B对应的数为b,且|a+4|+(b-3)2=0.
(1)则a=-4,b=3;并将这两个数在数轴上所对应的点A,B表示出来;
(2)数轴上在B点右边有一点C到A、B两点的距离和为11,若点C的数轴上所对应的数为x,求x的值;
(3)若点A,点B同时沿数轴向正方向运动,点A运动的速度为2单位/秒,点B运动的速度为1单位/秒,若|AB|=4,求运动时间t的值.
(温馨提示:M、N之间距离记作|MN|,点M、N在数轴上对应的数分别为m、n,则|MN|=|m-n|.)
分析 (1)利用绝对值的非负性质得到a+4=0,b-3=0,解方程即可求解;
(2)设点C在数轴上所对应的数为x,根据CA+CB=11列出方程,解方程即可;
(3)分A在点B的左边与A在点B的右边进行讨论求解.
解答 解:(1)∵且|a+4|+(b-3)2=0.
∴a+4=0,b-3=0,
解得a=-4,b=3.
点A、B表示在数轴上为:
故答案是:-4;3;
(2)设点C在数轴上所对应的数为x,
∵C在B点右边,
∴x>3.
根据题意得
x-3+x-(-4)=11,
解得x=5.
即点C在数轴上所对应的数为5;
(3)当A在点B的左边时,
2t-t=3-(-4)-4,
解得t=3;
当A在点B的右边时,
2t-t=3-(-4)+4,
解得t=11.
故运动时间t的值为3秒或11秒.
故答案为:-4,3.
点评 本题考查了一元一次方程的应用与数轴,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
相关题目
19.方程x2-7=0的根是( )
| A. | x=7 | B. | x1=7,x2=-7 | C. | x=$\sqrt{7}$ | D. | x1=-$\sqrt{7}$,x2=$\sqrt{7}$ |
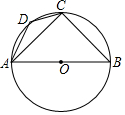 如图所示,AB是⊙O的直径,点C、D在⊙O上,若∠DAC=20°,∠B=50°,试求∠BCD的度数.
如图所示,AB是⊙O的直径,点C、D在⊙O上,若∠DAC=20°,∠B=50°,试求∠BCD的度数.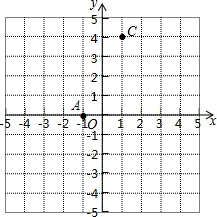 如图,A(-1,0),C(1,4),点B在x轴上,且AB=4.
如图,A(-1,0),C(1,4),点B在x轴上,且AB=4. 如图,在△ABC中,∠C=∠ABC=2∠A.
如图,在△ABC中,∠C=∠ABC=2∠A.