题目内容
18.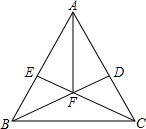 如图:在△ABC,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.求证:AF平分∠BAC.
如图:在△ABC,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.求证:AF平分∠BAC.
分析 先求证△AEC和△ADB全等,推出AE=AD,再求证△AEF和△ADF全等,可得EF=DF,进而可得推出AF平分∠BAC.
解答 证明:∵BD⊥AC于D,CE⊥AB于E,
∴∠AEC=∠ADB=90°,
在△ABD和△ACE中$\left\{\begin{array}{l}{∠BAC=∠BAC}\\{∠ADB=∠AEC}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△ACE(AAS),
∴AE=AD,
在Rt△AEF和Rt△ADF中$\left\{\begin{array}{l}{AE=AD}\\{AF=AF}\end{array}\right.$,
∴Rt△AEF≌Rt△ADF(HL),
∴EF=DF,
∴AF平分∠BAC.
点评 此题主要考查了全等三角形的判定与性质,以及角平分线的判定,关键是掌握到角两边距离相等的点在角的平分线上.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
6.方程x2-4x-3=0根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 有一个实数根 | D. | 没有实数根 |
10.-42的意义是( )
| A. | 2个-4相乘 | B. | 2个-4相加 | C. | 42的相反数 | D. | -4乘以2 |
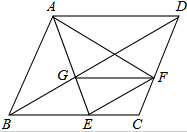 已知,如图,在菱形ABCD中,点E、F分别在边BC、CD,∠BAF=∠DAE,AE与BD交于点G.
已知,如图,在菱形ABCD中,点E、F分别在边BC、CD,∠BAF=∠DAE,AE与BD交于点G.