题目内容
6．方程x2-4x-3=0根的情况是（ ）| A． | 有两个不相等的实数根 | B． | 有两个相等的实数根 | ||
| C． | 有一个实数根 | D． | 没有实数根 |
分析 判断上述方程的根的情况，只要看根的判别式△=b2-4ac的值的符号就可以了．
解答 解：∵a=1，b=-4，c=-3，
∴△=b2-4ac=（-4）2-4×1×（-3）=28＞0，
∴方程有两个不相等的实数根．
故选A．
点评 本题考查了根的判别式，一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac有如下关系：
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．
练习册系列答案
相关题目
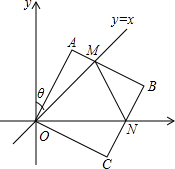在平面直角坐标中，边长为4的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上，点O在原点．现将正方形OABC绕O点顺时针旋转，旋转角为θ，当A点第一次落在直线y=x上时停止旋转．旋转过程中，AB边交直线y=x于点M，BC边交x轴于点N（如图）．
如图，在正方形ABCD时，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连结BD、DP，BD与CF相交于点H．则下列结论：①△ABE≌△DCF；②DP2=PH•PB；③$\frac{FP}{PH}=\frac{17}{30}$；④$\frac{{{S_{△BPD}}}}{{{S_{正方形ABCD}}}}=\frac{{\sqrt{3}-1}}{4}$．其中正确的是①②④（写出所有正确结论的序号）．
1．已知一元二次方程：①x2-2x-3=0，②x2+2x+3=0．下列说法正确的是（ ）
| A． | ①②都有实数解 | B． | ①无实数解，②有实数解 | ||
| C． | ①有实数解，②无实数解 | D． | ①②都无实数解 |
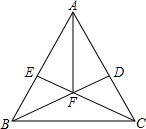如图：在△ABC，AB=AC，BD⊥AC于D，CE⊥AB于E，BD、CE相交于F．求证：AF平分∠BAC．