题目内容
8.已知m,n是二次方程x2+2015x+7=0的两个根,求(m2+2014m+6)(n2+2016n+8)的值.分析 先根据根与系数的关系求得x1+x2及x1•x2的值;然后化简(m2+2014m+6)(n2+2016n+8);最后将其代入求值即可.
解答 解:∵m、n是方程x2+2015x+7=0的两个根,
∴m+n=-2015,mn=7;
∴m2+2015m+7=0,
n2+2015n+7=0,
原式=(-m-7+6)(n-7+8)
=-(m+1)(n+1)
=-(mn+m+n+1),
=-(7-2015+1)=2007.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.以及一元二次方程解得意义.

练习册系列答案
相关题目
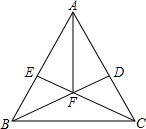 如图:在△ABC,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.求证:AF平分∠BAC.
如图:在△ABC,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.求证:AF平分∠BAC. 按照如图所示的操作步骤,若输入x的值为1,则输出的值为4.
按照如图所示的操作步骤,若输入x的值为1,则输出的值为4.