题目内容
19. 如图,在平行四边形ABCD中,点E为BC的中点,AE与对角线BD交于点F.
如图,在平行四边形ABCD中,点E为BC的中点,AE与对角线BD交于点F.(1)求证:DF=2BF;
(2)当∠AFB=90°且tan∠ABD=$\frac{1}{2}$时,若CD=$\sqrt{5}$,求AD长.
分析 (1)证明△BEF∽△DAF,得出对应边成比例,即可得出结论;
(2)求出tan∠ABD=$\frac{AF}{BF}$=$\frac{1}{2}$,设AF=x,则BF=2x,由勾股定理求出x=1,AF=1,BF=2,得出DF=4,再由勾股定理即可得出答案.
解答 (1)证明:∵四边形ABCD为平行四边形∴AD∥BC,AD=BC,AB=CD,
∵点E为BC的中点,
∴BE=$\frac{1}{2}$BC=$\frac{1}{2}$AD,
∵AD∥BC,
∴△BEF∽△DAF,
∴$\frac{BE}{AD}=\frac{BF}{DF}$=$\frac{1}{2}$,
∴DF=2BF
(2)解:∵CD=$\sqrt{5}$,
∴AB=CD=$\sqrt{5}$,
∵在Rt△ABF中,∠AFB=90°,∴tan∠ABD=$\frac{AF}{BF}$=$\frac{1}{2}$,
∴设AF=x,则BF=2x,
∴AB=$\sqrt{A{F}^{\;}2+B{F}^{2}}$=$\sqrt{5}$x=$\sqrt{5}$,
∴x=1,AF=1,BF=2,
∵DF=2BF,
∴DF=4,
∴AD=$\sqrt{A{F}^{2}+D{F}^{2}}$=$\sqrt{17}$.
点评 本题考查了平行四边形的性质、相似三角形的判定与性质、勾股定理,掌握平行四边形的对边平等且相等和相似三角形的判定与性质是解题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
14.初三(1)班体育委员统计本班30名同学体育中考成绩数据如下表所示:
则这30名同学成绩的众数和中位数分别是( )
| 成绩 | 25 | 26 | 27 | 28 | 29 | 30 |
| 人数 | 2 | 3 | 5 | 6 | 10 | 4 |
| A. | 29,30 | B. | 29,28 | C. | 28,30 | D. | 28,28 |
4.下列图形中,正方体展开后得到的图形不可能是( )
| A. |  | B. |  | C. |  | D. |  |
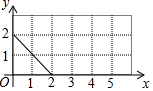 如图,动点P从(0,2)出发,沿所示的方向在矩形网格中运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,若第一次碰到矩形的边时坐标为P1(2,0),则P2017的坐标为(2,0).
如图,动点P从(0,2)出发,沿所示的方向在矩形网格中运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,若第一次碰到矩形的边时坐标为P1(2,0),则P2017的坐标为(2,0).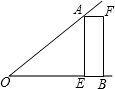 如图,已知∠AOB,OA=OB,点E在OB 上,四边形AEBF是矩形.
如图,已知∠AOB,OA=OB,点E在OB 上,四边形AEBF是矩形. 如图,Rt△ABC≌Rt△DCB,两斜边交于点O,如果AC=3,那么OD的长为1.5.
如图,Rt△ABC≌Rt△DCB,两斜边交于点O,如果AC=3,那么OD的长为1.5.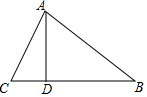 如图,在△ABC中,CD=$\sqrt{3}$,AB=5,AC=2$\sqrt{3}$,AD是BC边上的高,求BC的长.
如图,在△ABC中,CD=$\sqrt{3}$,AB=5,AC=2$\sqrt{3}$,AD是BC边上的高,求BC的长. 台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点C为一海港,且点 C与直线 AB上两点A,B的距离分别为300km和400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域.
台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点C为一海港,且点 C与直线 AB上两点A,B的距离分别为300km和400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域.