题目内容
10.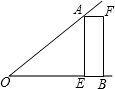 如图,已知∠AOB,OA=OB,点E在OB 上,四边形AEBF是矩形.
如图,已知∠AOB,OA=OB,点E在OB 上,四边形AEBF是矩形.(1)请你只用无刻度的直尺在图中画出∠AOB的平分线(保留画图痕迹);
(2)若∠AOB=45°,OA=OB=2$\sqrt{2}$,求BE的长.
分析 (1)根据矩形的对角线相等且互相平分,运用三线合一即可画出∠AOB的平分线;
(2)根据矩形AEBF中,AE⊥OB,∠AOB=45°,可得OE=cos45°×2$\sqrt{2}$=2,即可得出EB=2$\sqrt{2}$-2.
解答 解:(1)如图所示,OP即为所求;
(2)在矩形AEBF中,AE⊥OB,∠AOB=45°,
∴OE=cos45°×2$\sqrt{2}$=2,
∴EB=2$\sqrt{2}$-2.
点评 本题主要考查了角平分线的作图,等腰三角形的性质以及矩形的性质的运用,解题时注意:矩形的对角线相等且互相平分.

练习册系列答案
相关题目
5.2017年1月,在揭阳市第六届人民代表大会会议上,陈市长指出了,2016年预计全市生产总值2012亿元.请你将揭阳市全市生产总值(单位:亿元)用科学记数法来表示( )
| A. | 20.12×102 | B. | 0.2012×104 | C. | 2.012×103 | D. | 2.012×104 |
2.据报道,到2020年北京地铁规划线网将由19条线路组成,总长度将达到561500米,将561500用科学记数法表示为( )
| A. | 0.5615×106 | B. | 5.615×105 | C. | 56.15×104 | D. | 561.5×103 |
 某海域有A、B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求:
某海域有A、B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求: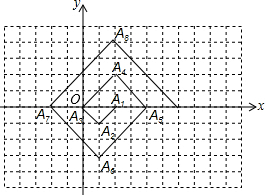 如图,在单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上,斜边长分别为2,4,6,…都是斜边在x轴上,斜边长分别为2,4,6,…,的等腰直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图所示规律,A2017的纵坐标为0.
如图,在单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上,斜边长分别为2,4,6,…都是斜边在x轴上,斜边长分别为2,4,6,…,的等腰直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图所示规律,A2017的纵坐标为0. 如图,在平行四边形ABCD中,点E为BC的中点,AE与对角线BD交于点F.
如图,在平行四边形ABCD中,点E为BC的中点,AE与对角线BD交于点F.