题目内容
12．
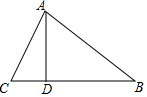如图，在△ABC中，CD=$\sqrt{3}$，AB=5，AC=2$\sqrt{3}$，AD是BC边上的高，求BC的长．
分析 直接利用勾股定理得出AD的长，进而求出BD的长，即可得出答案．
解答 解：∵AD是BC边上的高，CD=$\sqrt{3}$，AC=2$\sqrt{3}$，
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{（2\sqrt{3}）^{2}-（\sqrt{3}）^{2}}$=3，
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4，
∴BC=BD+CD=4+$\sqrt{3}$．
点评 此题主要考查了勾股定理，正确应用勾股定理是解题关键．
练习册系列答案
相关题目
某海域有A、B两个港口，B港口在A港口北偏西30°方向上，距A港口60海里，有一艘船从A港口出发，沿东北方向行驶一段距离后，到达位于B港口南偏东75°方向的C处，求：
如图，在平行四边形ABCD中，点E为BC的中点，AE与对角线BD交于点F．
7．
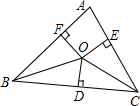如图，O是△ABC内一点，且O到三边AB、BC、CA的距离OF=OD=OE，若∠BAC=100°，则∠BOC等于（ ）
如图，O是△ABC内一点，且O到三边AB、BC、CA的距离OF=OD=OE，若∠BAC=100°，则∠BOC等于（ ）| A． | 140° | B． | 145° | C． | 150° | D． | 155° |
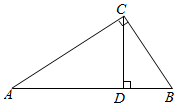如图，在Rt△ACB中，∠ACB=90°，CD⊥AB于D，AC=2，CD=1，则线段BC=$\frac{2\sqrt{3}}{3}$．