题目内容
如图，四边形ABCD中，AD=AB，∠ABC=∠ADC=90°，∠ACB=55°，则∠DAB的度数为考点：全等三角形的判定与性质
专题：
分析：先求出∠BAC，再根据HL证明Rt△ADC≌Rt△ABC，得出∠DAC=∠BAC，即可得出结果．
解答：
解：∵∠ABC=90°，∠ACB=55°，
∴∠BAC=90°-55°=35°，
在Rt△ADC和Rt△ABC中，
，
∴Rt△ADC≌Rt△ABC（HL），
∴∠DAC=∠BAC=35°，
∴∠DAB=∠DAC+∠BAC=70°；
故答案为：70°．
∴∠BAC=90°-55°=35°，
在Rt△ADC和Rt△ABC中，
|
∴Rt△ADC≌Rt△ABC（HL），
∴∠DAC=∠BAC=35°，
∴∠DAB=∠DAC+∠BAC=70°；
故答案为：70°．
点评：本题考查了全等三角形的判定与性质；利用HL证明直角三角形全等是解决问题的关键．
练习册系列答案
相关题目
如图是我市环北路改造后一圆柱形输水管的横截面，阴影部分为有水部分，如果水面AB宽为4m，水面最深地方的高度为1m，则该输水管的半径为（ ）| A、2m | B、2.5m |
| C、4m | D、5m |
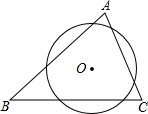如图所示，在△ABC中，∠A=70°，⊙O截△ABC的三条边所得的弦长相等，则∠BOC的度数为（ ）| A、125° | B、130° |
| C、135° | D、160° |
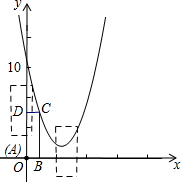在直角坐标系中，抛物线y=x2+bx+c经过点（0，10）和点（4，2）．
如图所示，在直角三角形ABC中，∠ACB=90°，BC=2，CD⊥AB，在AC上取一点E，使EC=BC，过点E作EF⊥AC交CD的延长线于点F．若EF=5，则AE=（ ）
如图，△ABC中，AB=AC，BD、CE是角平分线．