题目内容
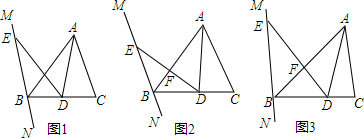
19. 已知:如图,点D在△ABC的BC边上,AC∥BE,BC=BE,∠ABC=∠E,求证:AB=DE.
已知:如图,点D在△ABC的BC边上,AC∥BE,BC=BE,∠ABC=∠E,求证:AB=DE.
分析 先利用平行线的性质得∠C=∠DBE,再根据“ASA”可证明△ABC≌△DEB,然后根据全等三角形的性质可得AB=DE.
解答 证明:∵BE∥AC,
∴∠C=∠DBE.
在△ABC和△DEB中,
$\left\{\begin{array}{l}∠C=∠DBE\\ BC=EB\\∠ABC=∠E\end{array}\right.$,
∴△ABC≌△DEB,
∴AB=DE.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在应用全等三角形的性质时主要是得到对应角相等或对应线段相等.

练习册系列答案
相关题目
10.菱形的边长为5,一条对角线长为8,则此菱形的面积是( )
| A. | 24 | B. | 30 | C. | 40 | D. | 48 |
14. 如图,四边形ABCD内接于⊙O,∠BCD=120°,则∠BAD的度数是( )
如图,四边形ABCD内接于⊙O,∠BCD=120°,则∠BAD的度数是( )
 如图,四边形ABCD内接于⊙O,∠BCD=120°,则∠BAD的度数是( )
如图,四边形ABCD内接于⊙O,∠BCD=120°,则∠BAD的度数是( )| A. | 30° | B. | 60° | C. | 80° | D. | 120° |
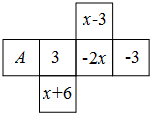 如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体相对的两个面所标注的值均互为相反数,求字母A所标注的值.
如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体相对的两个面所标注的值均互为相反数,求字母A所标注的值.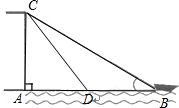 已知:如图,有人在岸上点C的地方,用绳子拉船靠岸,开始时,绳长CB=10米,CA⊥AB,且CA=6米,拉动绳子将船从点B沿BA方向行驶到点D后,绳长CD=6$\sqrt{2}$米.
已知:如图,有人在岸上点C的地方,用绳子拉船靠岸,开始时,绳长CB=10米,CA⊥AB,且CA=6米,拉动绳子将船从点B沿BA方向行驶到点D后,绳长CD=6$\sqrt{2}$米.