Question

11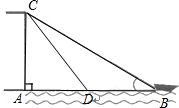．已知：如图，有人在岸上点C的地方，用绳子拉船靠岸，开始时，绳长CB=10米，CA⊥AB，且CA=6米，拉动绳子将船从点B沿BA方向行驶到点D后，绳长CD=6$\sqrt{2}$米．
（1）试判定△ACD的形状，并说明理由；
（2）求船体移动距离BD的长度．

Answer 1

分析 （1）直接利用勾股定理得出AD的长，进而得出△ACD的形状；
（2）利用勾股定理得出AB的长，进而得出BD的长．

解答 解：（1）由题意可得：AC=6m，DC=6$\sqrt{2}$m，∠CAD=90°，
可得AD=$\sqrt{C{D}^{2}-A{C}^{2}}$=6（m），
故△ACD是等腰直角三角形；

（2）∵AC=6m，BC=10m，∠CAD=90°，
∴AB=$\sqrt{B{C}^{2}-A{C}^{2}}$=8（m），
则BD=AB-AD=8-6=2（m）．
答：船体移动距离BD的长度为2m．

点评 此题主要考查了勾股定理的应用，根据题意正确应用勾股定理是解题关键．