题目内容
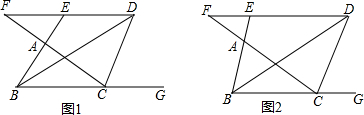
 如图,已知△ABC中,BD平分∠ABC,点M是线段BD上一点,过M点作EF∥BC,分别交边AB、AC于点E、F,作MN∥AB交BC于点N.
如图,已知△ABC中,BD平分∠ABC,点M是线段BD上一点,过M点作EF∥BC,分别交边AB、AC于点E、F,作MN∥AB交BC于点N.(1)试判断四边形BEMN是什么特殊四边形?并说明你的理由.
(2)若BA=BC,连接EN,四边形EFCN是平行四边形吗?为什么?
考点:平行四边形的判定
专题:
分析:(1)因为四边形BEMN的对边都互相平行很容易得到是平行四边形,又因为BD平分∠ABC,所以很容易证得△BEM是等腰三角形所以BE=EM,所以四边形BEMN是菱形;
(2)根据BA=BC,BD平分∠ABC得到BD⊥AC,根据四边形BEMN是菱形得到AC∥EN,利用两组对边平行的四边形是平行四边形判定平行四边形即可.
(2)根据BA=BC,BD平分∠ABC得到BD⊥AC,根据四边形BEMN是菱形得到AC∥EN,利用两组对边平行的四边形是平行四边形判定平行四边形即可.
解答:解:(1)四边形BEMN是菱形,
∵EF∥BC,MN∥AB,
∴四边形BEMN是平行四边形,
∵EF∥BC,
∴∠EMB=∠MBN,
又∵∠EBM=∠MBN,
∴∠EMB=∠EBM,
∴EB=EM,
∴平行四边形BEMN是菱形;
(2)∵BA=BC,BD平分∠ABC,
∴BD⊥AC,
∵四边形BEMN是菱形,
∴BD⊥EN,
∴AC∥EN,
又∵EF∥CN,
∴四边形EFCN是平行四边形.
∵EF∥BC,MN∥AB,
∴四边形BEMN是平行四边形,
∵EF∥BC,
∴∠EMB=∠MBN,
又∵∠EBM=∠MBN,
∴∠EMB=∠EBM,
∴EB=EM,
∴平行四边形BEMN是菱形;
(2)∵BA=BC,BD平分∠ABC,
∴BD⊥AC,
∵四边形BEMN是菱形,
∴BD⊥EN,
∴AC∥EN,
又∵EF∥CN,
∴四边形EFCN是平行四边形.
点评:考查了平行四边形的判定及菱形的性质,解题的关键是了解有关的判定定理,难度不大.

练习册系列答案
相关题目
下列说法不正确的是( )
| A、0既不是正数,也不是负数 |
| B、互为相反数的两个数的和为0 |
| C、互为倒数的两个数的和为1 |
| D、0的绝对值是0 |
 如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC,CF⊥DE于F,求证:CF平分∠DCE.
如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC,CF⊥DE于F,求证:CF平分∠DCE.