题目内容
 如图矩形ABCD中,AB=6,BC=8,若将矩形折叠,使B点与D点重合,求折痕EF的长.
如图矩形ABCD中,AB=6,BC=8,若将矩形折叠,使B点与D点重合,求折痕EF的长.考点:翻折变换(折叠问题)
专题:
分析:如图,证明BF=DF(设为λ),BD⊥EF;证明∠C=90°,DC=AB=6,FC=8-λ;列出关于λ的方程,求出λ;借助面积公式即可解决问题.
解答: 解:如图,连接BE,DF;
解:如图,连接BE,DF;
由题意得:BF=DF(设为λ),BD⊥EF;
∵四边形ABCD为矩形,
∴∠C=90°,DC=AB=6,FC=8-λ;
由勾股定理得:λ2=(8-λ)2+62,
解得:λ=
;BF=λ=
.
同理可求:BD=10.
∵S四边形BEDF=BF•DC=
BD•EF,
∴EF=7.5.
 解:如图,连接BE,DF;
解:如图,连接BE,DF;由题意得:BF=DF(设为λ),BD⊥EF;
∵四边形ABCD为矩形,
∴∠C=90°,DC=AB=6,FC=8-λ;
由勾股定理得:λ2=(8-λ)2+62,
解得:λ=
| 25 |
| 4 |
| 25 |
| 4 |
同理可求:BD=10.
∵S四边形BEDF=BF•DC=
| 1 |
| 2 |
∴EF=7.5.
点评:该题主要考查了翻折变换的性质及其应用问题;解题的关键是作辅助线,灵活运用翻折变换的性质、勾股定理等几何知识点来分析、判断、推理或解答.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
下列说法不正确的是( )
| A、0既不是正数,也不是负数 |
| B、互为相反数的两个数的和为0 |
| C、互为倒数的两个数的和为1 |
| D、0的绝对值是0 |
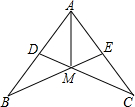 如图,AB=AC,AD=AE,∠BAC=60°,∠C=25°,则∠BMD的度数为( )
如图,AB=AC,AD=AE,∠BAC=60°,∠C=25°,则∠BMD的度数为( )| A、50° | B、65° |
| C、70° | D、85° |
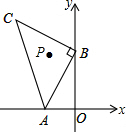 如图,已知点A(a,0),B(0,b),且(a+2)2+|b-4|=0,以B点为直角顶点在第二象限作等腰直角△ABC.
如图,已知点A(a,0),B(0,b),且(a+2)2+|b-4|=0,以B点为直角顶点在第二象限作等腰直角△ABC.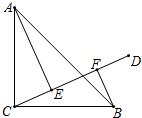 如图,在△ABC中,∠ABC=90°,AC=BC,AE⊥CD,BF⊥CD,垂足分别为点E,F,图中BF与哪条线段相等?说明理由.
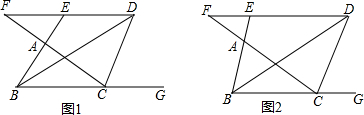
如图,在△ABC中,∠ABC=90°,AC=BC,AE⊥CD,BF⊥CD,垂足分别为点E,F,图中BF与哪条线段相等?说明理由. 如图,已知正方形ABCD中,E是BC的中点,F是CD上一点,且FD=3CF,试判断△AEF的形状,并说明理由.
如图,已知正方形ABCD中,E是BC的中点,F是CD上一点,且FD=3CF,试判断△AEF的形状,并说明理由.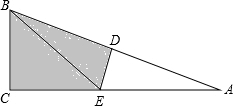 如图,在Rt△ABC中,∠C=90°,△ABC沿DE折叠,使得点A落在点B处,已知AC=6,BC=2,则四边形BCED的面积为
如图,在Rt△ABC中,∠C=90°,△ABC沿DE折叠,使得点A落在点B处,已知AC=6,BC=2,则四边形BCED的面积为