题目内容
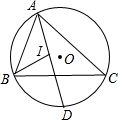 如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于D,∠ABC的平分线交直线AD于I.
如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于D,∠ABC的平分线交直线AD于I.(1)写出∠BID与∠C的关系,并证明;
(2)若∠ABC的外角平分线交直线AD于I,其余条件不变,则∠BID与∠ACB有何关系?试证明.
考点:圆周角定理
专题:证明题
分析:(1)根据角平分线的性质得∠BAI=
∠BAC,∠ABI=
∠ABC,然后根据三角形外角性质得到∠BID=∠BAI+∠ABI=
(∠ABC+∠ABC),再利用三角形内角和定理易得∠BID=90°-
∠C;
(2)如图,利用角平分线的定义得到∠BAI=
∠BAC,∠EBI=
∠EBC,再利用三角形外角性质得∠EBC=∠BID+∠BAI,∠EBC=∠BAC+∠C,然后利用等式的性质即可得到∠BID=
∠C.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)如图,利用角平分线的定义得到∠BAI=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:(1)∠BID=90°-
解:(1)∠BID=90°-
∠C.理由如下:
∵IA平分∠BAC,IB平分∠ABC,
∴∠BAI=
∠BAC,∠ABI=
∠ABC,
∴∠BID=∠BAI+∠ABI=
(∠ABC+∠ABC)=
(180°-∠C)=90°-
∠C;
(2)∠BID=
∠ACB.理由如下:
如图,∵IA平分∠BAC,IB平分∠EBC,
∴∠BAI=
∠BAC,∠EBI=
∠EBC,
∵∠EBC=∠BID+∠BAI,
∠EBC=∠BAC+∠C,
∴2∠BID+2∠BAI=∠BAC+∠C,
∴∠BID=
∠C.
 解:(1)∠BID=90°-
解:(1)∠BID=90°-| 1 |
| 2 |
∵IA平分∠BAC,IB平分∠ABC,
∴∠BAI=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BID=∠BAI+∠ABI=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)∠BID=
| 1 |
| 2 |
如图,∵IA平分∠BAC,IB平分∠EBC,
∴∠BAI=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠EBC=∠BID+∠BAI,
∠EBC=∠BAC+∠C,
∴2∠BID+2∠BAI=∠BAC+∠C,
∴∠BID=
| 1 |
| 2 |
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了角平分线的定义和三角形外角性质.

练习册系列答案
相关题目
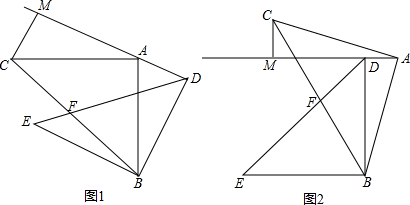
 如图,把一个长方形的纸片沿EF折叠后,点D、C分别落在点M、N的位置,如果∠EFB=65°,那么∠AEM等于
如图,把一个长方形的纸片沿EF折叠后,点D、C分别落在点M、N的位置,如果∠EFB=65°,那么∠AEM等于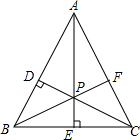 如图,△ABC边AB、BC的垂直平分线交于点P.
如图,△ABC边AB、BC的垂直平分线交于点P. 如图所示,将△ABC沿直线BC方向平移△DEF的位置,G是DE上一点,连接AG,过点A、D作直线MN.
如图所示,将△ABC沿直线BC方向平移△DEF的位置,G是DE上一点,连接AG,过点A、D作直线MN.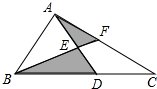 如图所示,阴影部分的面积是2cm2,AE=ED,BD=2DC,则△ABC的面积是
如图所示,阴影部分的面积是2cm2,AE=ED,BD=2DC,则△ABC的面积是