题目内容
Rt△ABC的斜边AB=6cm,直角边AC=3cm,以C为圆心,2cm为半径的圆和AB的位置关系是 ,4cm为半径的圆和AB的位置关系是 ;若和AB相切,则圆的半径长为 .
考点:直线与圆的位置关系
专题:
分析:先根据勾股定理求出BC的长,再根据三角形的面积公式求出点C到直线AB的距离,根据直线与圆的位置关系即可得出结论.
解答:解:∵Rt△ABC的斜边AB=6cm,直角边AC=3cm,
∴BC=
=3
,
设点C到直线AB的距离为h,则h=
=
(cm),
∵2cm<
cm,4cm>
cm,
∴以C为圆心,2cm为半径的圆和AB的位置关系是相离;4cm为半径的圆和AB的位置关系是相交;若和AB相切,则圆的半径长为
cm.
故答案为:相离,相交,
cm.
∴BC=
| 62-32 |
| 3 |
设点C到直线AB的距离为h,则h=
3×3
| ||
| 6 |
3
| ||
| 2 |
∵2cm<
3
| ||
| 2 |
3
| ||
| 2 |
∴以C为圆心,2cm为半径的圆和AB的位置关系是相离;4cm为半径的圆和AB的位置关系是相交;若和AB相切,则圆的半径长为
3
| ||
| 2 |
故答案为:相离,相交,
3
| ||
| 2 |
点评:本题考查的是直线与圆的位置关系,熟知判断直线和圆的位置关系时设⊙O的半径为r,圆心O到直线l的距离为d.当d<r时,直线l和⊙O相交;当d=r时,直线l和⊙O相切;当d>r时,直线l和⊙O相离是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列方程中,解是2的方程是( )
| A、2x+2=4 | ||||
| B、6-2x=-2 | ||||
C、9-
| ||||
D、
|
 如图,把一个长方形的纸片沿EF折叠后,点D、C分别落在点M、N的位置,如果∠EFB=65°,那么∠AEM等于
如图,把一个长方形的纸片沿EF折叠后,点D、C分别落在点M、N的位置,如果∠EFB=65°,那么∠AEM等于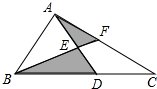 如图所示,阴影部分的面积是2cm2,AE=ED,BD=2DC,则△ABC的面积是
如图所示,阴影部分的面积是2cm2,AE=ED,BD=2DC,则△ABC的面积是 如图,点C是
如图,点C是
 如图,在△ABC中,D为AB的延长线上一点,且BD=AC,∠ACB=∠ABC,E是AB的中点,连接CD,CE.求证:CE=
如图,在△ABC中,D为AB的延长线上一点,且BD=AC,∠ACB=∠ABC,E是AB的中点,连接CD,CE.求证:CE=