题目内容
已知关于x的方程mx2-(m+2)x+2=0(m≠0).
(1)求证:方程总有两个实数根;
(2)已知方程有两个不相等的实数根α,β满足
+
=2,求m的值.
(1)求证:方程总有两个实数根;
(2)已知方程有两个不相等的实数根α,β满足
| 1 |
| α |
| 1 |
| β |
考点:根的判别式,根与系数的关系
专题:
分析:(1)求得方程根的判别式,证明其总大于或等于0即可;
(2)利用根与系数的关系分别求得αβ和α+β,代入可得到关于m的方程,求其即可.
(2)利用根与系数的关系分别求得αβ和α+β,代入可得到关于m的方程,求其即可.
解答:(1)证明:
∵△=(m+2)2-8m=m2+4m+4-8m=m2-4m+4=(m-2)2≥0,
∴方程总有两个实数要;
(2)解:
∵方程有两个不相等的实数根α,β,
∴由根与系数的关系可得α+β=
,αβ=
,
∵
+
=
=2,
∴
=2,
解得m=2.
∵△=(m+2)2-8m=m2+4m+4-8m=m2-4m+4=(m-2)2≥0,
∴方程总有两个实数要;
(2)解:
∵方程有两个不相等的实数根α,β,
∴由根与系数的关系可得α+β=
| m+2 |
| m |
| 2 |
| m |
∵
| 1 |
| α |
| 1 |
| β |
| α+β |
| αβ |
∴
| ||
|
解得m=2.
点评:本题主要考查一元二次方程根的判别及根与系数的关系,掌握一元二次方程根的判别式与根的情况是解题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
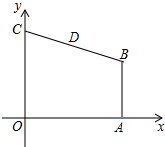 已知:如图,在直角梯形COAB中,OC∥AB,∠AOC=90°,AB=4,AO=8,OC=10,以O为原点建立平面直角坐标系,点D为线段BC的中点.动点P从点A出发,以每秒4个单位的速度,沿折线AO-OC-CD向终点D运动,设运动时间为t秒.
已知:如图,在直角梯形COAB中,OC∥AB,∠AOC=90°,AB=4,AO=8,OC=10,以O为原点建立平面直角坐标系,点D为线段BC的中点.动点P从点A出发,以每秒4个单位的速度,沿折线AO-OC-CD向终点D运动,设运动时间为t秒.