题目内容
11. 如图,△ABC中,BF是高,延长CB至点D,使BD=BA,连接AD,过点D作DE⊥AB交AB的延长线于点E,当AF=BE,∠CAD=96°时,∠C=56°.
如图,△ABC中,BF是高,延长CB至点D,使BD=BA,连接AD,过点D作DE⊥AB交AB的延长线于点E,当AF=BE,∠CAD=96°时,∠C=56°.
分析 根据已知条件得到∠E=∠AFB=90°,推出Rt△BED≌△RtABF,根据全等三角形的性质得到∠DBE=∠BAF,等量代换得到∠BDA=∠BAD,根据三角形的外角的性质得到∠CAB=2∠BAD,根据已知条件即可得到结论.
解答 解:∵BF是高,DE⊥AB,
∴∠E=∠AFB=90°,
在Rt△BED与△RtABF中,
$\left\{\begin{array}{l}{BD=AB}\\{BE=AF}\end{array}\right.$,
∴Rt△BED≌△RtABF,
∴∠DBE=∠BAF,
∵∠DBE=∠ABC,
∴∠CBA=∠CAB,
∵AB=BD,
∴∠BDA=∠BAD,
∵∠CBA=∠BDA+∠BAD,
∴∠CBA=2∠BAD,
∴∠CAB=2∠BAD,
∴∠CAB=$\frac{2}{3}$∠CAD,
∵∠CAD=96°,
∴∠CAB=64°,
∴∠C=180°-2∠CAB=52°.
故答案为:52°.
点评 本题考查了全等三角形的判定和性质,等腰三角形的性质,三角形的内角和,熟练掌握全等三角形的判定定理是解题的关键.

练习册系列答案
相关题目
19.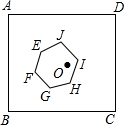 如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个六边形的边长最大时,AE的最小值为( )
如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个六边形的边长最大时,AE的最小值为( )
 如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个六边形的边长最大时,AE的最小值为( )
如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个六边形的边长最大时,AE的最小值为( )| A. | $\frac{\sqrt{2}+1}{2}$ | B. | $\frac{\sqrt{2}-1}{2}$ | C. | $\frac{3+2\sqrt{3}}{6}$ | D. | $\frac{3-2\sqrt{3}}{6}$ |
1.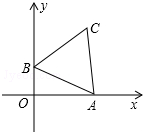 如图,边长为2的等边△ABC的顶点A,B分别在x轴正半轴和y轴正半轴上运动,则动点C到原点O的距离的最大值是( )
如图,边长为2的等边△ABC的顶点A,B分别在x轴正半轴和y轴正半轴上运动,则动点C到原点O的距离的最大值是( )
 如图,边长为2的等边△ABC的顶点A,B分别在x轴正半轴和y轴正半轴上运动,则动点C到原点O的距离的最大值是( )
如图,边长为2的等边△ABC的顶点A,B分别在x轴正半轴和y轴正半轴上运动,则动点C到原点O的距离的最大值是( )| A. | $\sqrt{3}-1$ | B. | $\sqrt{3}+1$ | C. | $\sqrt{6}-1$ | D. | $\sqrt{6}+1$ |
 如图,△ABC内接于圆,点D是AC上一点,将∠A沿BD翻折,点A正好落在圆上点E处.若∠C=50°,则∠ABE的度数为80°.
如图,△ABC内接于圆,点D是AC上一点,将∠A沿BD翻折,点A正好落在圆上点E处.若∠C=50°,则∠ABE的度数为80°.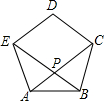 己知:如图,正五边形的对角线AC和BE相交于点P.求证:
己知:如图,正五边形的对角线AC和BE相交于点P.求证: