题目内容
(1)如图1,已知AB是⊙O的直径,弦CD丄AB于E,AC=8,CD=6,求cos∠ABC的值.

(2)如图,在△ABC中,∠A=30°,∠B=45s,AC=2
,求AB的长.

(2)如图,在△ABC中,∠A=30°,∠B=45s,AC=2
| 3 |
考点:垂径定理,圆周角定理,解直角三角形
专题:计算题
分析:(1)根据垂径定理由CD丄AB得CE=
CD=3,则根据余弦定义得cos∠ACE=
,再根据圆周角定理由AB是⊙O的直径得到∠ACB=90°,然后根据等角的余角相等得到∠B=∠ACE,所以cos∠ABC=
;
(2)作CD⊥AB于D,在Rt△ACD中,根据含30度的直角三角形三边的关系得CD=
AC=
,AD=
CD=3,在Rt△BCD中,根据等腰直角三角形的性质得∴BD=CD=
,于是得到AB=AD+BD=3+
.
| 1 |
| 2 |
| 3 |
| 8 |
| 3 |
| 8 |
(2)作CD⊥AB于D,在Rt△ACD中,根据含30度的直角三角形三边的关系得CD=
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
解答:解: (1)∵CD丄AB,
(1)∵CD丄AB,
∴CE=DE=
CD=
×6=3,
∴cos∠ACE=
=
,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠B+∠A=90°,
而∠ACE+∠A=90°,
∴∠B=∠ACE,
∴cos∠ABC=
;
(2)作CD⊥AB于D,如图2,
在Rt△ACD中,AC=2
,∠A=30°,
∴CD=
AC=
,
AD=
CD=3,
在Rt△BCD中,∠B=45°,
∴BD=CD=
,
∴AB=AD+BD=3+
.
 (1)∵CD丄AB,
(1)∵CD丄AB,∴CE=DE=
| 1 |
| 2 |
| 1 |
| 2 |
∴cos∠ACE=
| CE |
| AC |
| 3 |
| 8 |
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠B+∠A=90°,
而∠ACE+∠A=90°,
∴∠B=∠ACE,
∴cos∠ABC=
| 3 |
| 8 |
(2)作CD⊥AB于D,如图2,
在Rt△ACD中,AC=2
| 3 |
∴CD=
| 1 |
| 2 |
| 3 |
AD=
| 3 |
在Rt△BCD中,∠B=45°,
∴BD=CD=
| 3 |
∴AB=AD+BD=3+
| 3 |
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理和解直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列各数中,最大的数是( )
| A、-1 | ||
| B、2 | ||
| C、0 | ||
D、
|
 如图,AB是半圆的直径,点D是弧AC的中点,∠ABC=50°,则∠DAB的度数是
如图,AB是半圆的直径,点D是弧AC的中点,∠ABC=50°,则∠DAB的度数是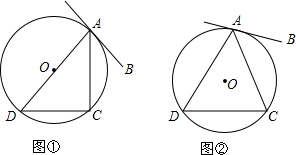 如图,直线AB切⊙O于点A,点C、D在⊙O上.试探求:
如图,直线AB切⊙O于点A,点C、D在⊙O上.试探求:
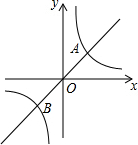 如图,定义:若双曲线y=
如图,定义:若双曲线y= 如图,在△ABC中,AB=AC,AD⊥BC,AE∥BC.
如图,在△ABC中,AB=AC,AD⊥BC,AE∥BC.