题目内容
16.若$\frac{m{x}^{2}}{{x}^{2}-{y}^{2}}$=$\frac{2xy-{y}^{2}}{{x}^{2}-{y}^{2}}$+$\frac{x-y}{x+y}$,则m=1.分析 已知等式右边通分并利用同分母分式的加法法则计算,利用分式相等的条件求出m的值即可.
解答 解:$\frac{m{x}^{2}}{{x}^{2}-{y}^{2}}$=$\frac{2xy-{y}^{2}}{{x}^{2}-{y}^{2}}$+$\frac{(x-y)^{2}}{{x}^{2}-{y}^{2}}$=$\frac{{x}^{2}}{{x}^{2}-{y}^{2}}$,
则m=1,
故答案为:1.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
1.估计下列事件发生的可能性的大小,①从装有1个红球和2个黄球的袋子中摸出的1个球是白球;②抛掷1枚质地均匀的骰子,向上一面的点数是偶数;③调查商场中的1位顾客,他是闰年出生的;④随意调查一位青年,他接受过九年制义务教育;⑤在地面上抛掷1个小石块,石块会落下.将这些事件的序号按发生的可能性从大到小的顺序排列,正确的是( )
| A. | ①②③④⑤ | B. | ⑤④③②① | C. | ⑤④②③① | D. | ④⑤③②① |
10.某市的电力紧缺,电力公司为鼓励市民节约用电,采取按月用电量分段收费办法,规定:若每月用电量不超过190度,收费标准为0.53元/度;若每月用电量为190度-290度,收费标准由两部分组成:①其中190度;按0.53元/度收费,②超出190度的部分按0.58元/度收费.现提供一居民某月电费发票的部分信息如下表所示:
根据以上提供信息解答下列问题:
(1)如果月用电量x度来表示,实付金额用y元来表示,请你写出实付金额用y元与月用电量x度之间的函数关系式;
(2)请你根据表中本月实付金额计算这个家庭本月的实际用电量;
(3)若小强和小华家一个月的实际用电量分别为120度和250度,则实付金额分别为多少元?
| Xxx居民电费专用发票 | |
| 计费期限:一个月 | |
| 用电量(度) | 电价(元/度) |
| 阶梯一:190 | 0.53 |
| 阶梯二:190-290(超出部分) | 0.58 |
| 本月实用金额:106.5(元) | (大写)壹佰零陆元伍角 |
(1)如果月用电量x度来表示,实付金额用y元来表示,请你写出实付金额用y元与月用电量x度之间的函数关系式;
(2)请你根据表中本月实付金额计算这个家庭本月的实际用电量;
(3)若小强和小华家一个月的实际用电量分别为120度和250度,则实付金额分别为多少元?
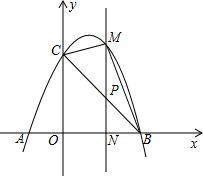 如图,抛物线y=-x2+2x+3与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,顶点为D,若点P为线段BC上的任意一点(点P不与B、C重合),M为抛物线上一点,且PM∥y轴.
如图,抛物线y=-x2+2x+3与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,顶点为D,若点P为线段BC上的任意一点(点P不与B、C重合),M为抛物线上一点,且PM∥y轴. 如图,在△ABC中,AD是角平分线,AE是高,∠BAC=40°,∠C=60°,求∠DAE的度数.
如图,在△ABC中,AD是角平分线,AE是高,∠BAC=40°,∠C=60°,求∠DAE的度数.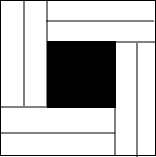 如图所示的正方形是由八块相同的长方形拼制而成的,且长与宽之比为4:1,中间留下一个边长为2mm的小正方形,你能求出长方形的长与宽吗?大正方形的面积是多少?
如图所示的正方形是由八块相同的长方形拼制而成的,且长与宽之比为4:1,中间留下一个边长为2mm的小正方形,你能求出长方形的长与宽吗?大正方形的面积是多少?