Question

8．等腰三角形一腰上的中线把该三角形的周长分为12.5cm和11.5cm两部分，求这个三角形各边的长？

Answer 1

分析 因为两个数据具体是哪一部分的不明确，所以分12.5cm是腰长加腰长的一半和11.5cm是腰长加腰长的一半两种情况讨论求解．

解答 解：如图：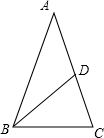

根据题意，
（1）若12.5cm是腰长加腰长的一半，
则腰长为：12.5×$\frac{2}{3}$=8$\frac{1}{3}$cm，
底边长为：11.5-8$\frac{1}{3}$×$\frac{1}{2}$=7$\frac{1}{3}$cm，
此时三角形的三边长为8$\frac{1}{3}$cm、8$\frac{1}{3}$cm、7$\frac{1}{3}$cm，
能组成三角形；

（2）若11.5cm是腰长加腰长的一半，
则腰长为：11.5×$\frac{2}{3}$=7$\frac{2}{3}$cm，
底边长为：12.5-$\frac{1}{2}$×7$\frac{2}{3}$=8$\frac{2}{3}$cm，
此时，三角形的三边长为7$\frac{2}{3}$cm、7$\frac{2}{3}$cm、8$\frac{2}{3}$cm，能组成三角形．
故这个三角形各边的长分别为8$\frac{1}{3}$cm、8$\frac{1}{3}$cm、7$\frac{1}{3}$cm或7$\frac{2}{3}$cm、7$\frac{2}{3}$cm、8$\frac{2}{3}$cm．

点评 本题考查了等腰三角形的性质；解题中应用了等腰三角形腰长相等的性质和分类讨论的思想，要注意根据三角形的三边关系判定是否能够组成三角形．