题目内容
6.在正方形ABCD外侧作直线AP,点B关于直线AP的对称点为E,连接BE,DE,其中DE交直线AP于点F.(1)①依题意补全图1;
②若∠PAB=20°,求∠ADF的度数;
(2)若设∠PAB=a,且0°<a<90°,求∠ADF的度数(直接写出结果,结果可用含a的代数式表示)
(3)如图2,若45°<∠PAB<90°,用等式表示线段AB、FE、FD之间的数量关系,并证明.

分析 (1)①根据题意直接画出图形得出即可;
②利用对称的性质以及等角对等边的性质,进而得出答案;
(2)利用对称的性质以及等角对等边进而得出答案;
(3)由轴对称的性质可得:,进而利用勾股定理得出答案.
解答 解:(1)①如图1所示:
②如图2,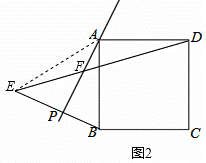
连接AE,由对称得,
∠PAB=∠PAE=20°,AE=AB=AD,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠EAP=∠BAP=20°,
∴∠EAD=130°,
∴∠ADF=$\frac{180°-130°}{2}$=25°;
(2)如图2,
连接AE,由对称得
∠PAB=∠PAE=α,AE=AB=AD,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠EAP=∠BAP=α,
∴∠EAD=90°+2α,
∴∠ADF=$\frac{180°-(90°+2α)}{2}$=45°-α.
(3)如图3,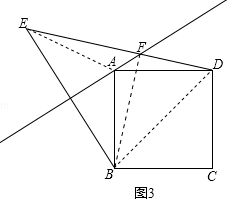
连接AE、BF、BD,
由对称可知,EF=BF,AE=AB=AD,
∠ABF=∠AEF=∠ADF,
∴∠BFD=∠BAD=90°,
在Rt△BDF中,BF2+FD2=BD2,
在Rt△ABC中,BD=$\sqrt{2}$AB,
∴EF2+FD2=2AB2.
点评 此题是四边形综合题,主要考查了正方形的性质以及勾股定理和等腰三角形的性质等知识,利用轴对称的性质得出对应边相等是解题关键.

练习册系列答案
相关题目
17.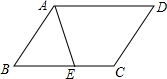 如图,在?ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于( )
如图,在?ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于( )
 如图,在?ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于( )
如图,在?ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于( )| A. | 4cm | B. | 3cm | C. | 2cm | D. | 1cm |
1. 如图,AB∥CD,CE平分∠ACD,若∠2=70°,那么∠1=( )
如图,AB∥CD,CE平分∠ACD,若∠2=70°,那么∠1=( )
 如图,AB∥CD,CE平分∠ACD,若∠2=70°,那么∠1=( )
如图,AB∥CD,CE平分∠ACD,若∠2=70°,那么∠1=( )| A. | 70° | B. | 50° | C. | 35° | D. | 25° |
18.以下问题,不适合用普查的是( )
| A. | 了解全班同学每周体育锻炼的时间 | |
| B. | 为了了解“嫦娥二号”卫星零部件的状况 | |
| C. | 学校招聘教师,对应聘人员面试 | |
| D. | 了解一批灯泡的使用寿命 |
15.实数-3的绝对值是( )
| A. | 3 | B. | -3 | C. | 0 | D. | ±$\sqrt{3}$ |
 如图,在平行四边形ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,平行四边形ABCD的周长是14,则DM等于3.
如图,在平行四边形ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,平行四边形ABCD的周长是14,则DM等于3.