题目内容
13.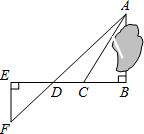 为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据,根据所测数据不能求出A,B间距离的是( )
为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据,根据所测数据不能求出A,B间距离的是( )| A. | BC,∠ACB | B. | DE,DC,BC | C. | EF,DE,BD | D. | CD,∠ACB,∠ADB |
分析 根据三角形相似可知,要求出AB,只需求出EF即可.所以借助于相似三角形的性质,根据$\frac{EF}{AB}=\frac{FD}{BD}$即可解答.
解答 解:此题比较综合,要多方面考虑,
A、因为知道∠ACB和BC的长,所以可利用∠ACB的正切来求AB的长;
B、无法求出A,B间距离.
C、因为△ABD∽△EFD,可利用$\frac{EF}{AB}=\frac{FD}{BD}$,求出AB;
D、可利用∠ACB和∠ADB的正切求出AB;
据所测数据不能求出A,B间距离的是选项B;
故选:B.
点评 本题考查相似三角形的应用和解直角三角形的应用;将实际问题转化为数学问题是解决问题的关键.

练习册系列答案
相关题目
1.在△ABC中,BC=15cm,CA=45cm,AB=57cm,另一个和它相似的三角形的最短边长是5cm,则最长边长是
( )
( )
| A. | 18cm | B. | 19cm | C. | 24cm | D. | 19.5cm |
18.化简a-[b-2a-(a-b)]的结果是( )
| A. | -2a | B. | 2a | C. | 4a-2b | D. | 2a-2b |
2.已知点P到∠AOB两边的距离相等,若∠POB=45°,则∠AOB等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
 如图,AB是⊙O直径,切线CA与⊙O相切于点A,点D在⊙O上,且OD⊥OC,
如图,AB是⊙O直径,切线CA与⊙O相切于点A,点D在⊙O上,且OD⊥OC,