题目内容
 如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB∥DE,AB=DE,AC=DF.求证:BC=EF.
如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB∥DE,AB=DE,AC=DF.求证:BC=EF.考点:全等三角形的判定与性质
专题:证明题
分析:根据平行线的性质推出∠A=∠D,根据SAS推出△ABC≌△DEF,根据全等三角形的性质推出即可.
解答:证明:∵AB∥DE,
∴∠A=∠D,
在△ABC和△DEF中
∴△ABC≌△DEF,
∴BC=EF.
∴∠A=∠D,
在△ABC和△DEF中
|
∴△ABC≌△DEF,
∴BC=EF.
点评:本题考查了全等三角形的性质和判定,平行线的性质的应用,解此题的关键是推出△ABC≌△DEF,注意:全等三角形的对应边相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
关于x的一元二次方程ax2+bx+c=0(a≠0),下列命题:
①若a、c异号,则方程 ax2+bx+c=0必有两个不相等的实数根;
②若4a-2b+c=0,则方ax2+bx+c=0有两个不等实根;
③若方程ax2+bx+c=0的两根互为相反数,则b=0;
④若b=a+c,则ax2+bx+c=0方程有两个不相等的实数根.
其中正确的为( )
①若a、c异号,则方程 ax2+bx+c=0必有两个不相等的实数根;
②若4a-2b+c=0,则方ax2+bx+c=0有两个不等实根;
③若方程ax2+bx+c=0的两根互为相反数,则b=0;
④若b=a+c,则ax2+bx+c=0方程有两个不相等的实数根.
其中正确的为( )
| A、①③ | B、①②③ |
| C、②③④ | D、①③④ |
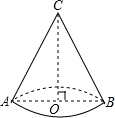 亮亮同学为了参加兰州市第十届中小学生艺术节,用纸板制作了一个圆锥形纸帽,如图所示,它的底面半径0B=9,高0C=12. 若不计损耗,则这个圆锥形纸帽的侧面积是
亮亮同学为了参加兰州市第十届中小学生艺术节,用纸板制作了一个圆锥形纸帽,如图所示,它的底面半径0B=9,高0C=12. 若不计损耗,则这个圆锥形纸帽的侧面积是( )
| A、90π | B、120π |
| C、135π | D、150π |