题目内容
关于x的一元二次方程ax2+bx+c=0(a≠0),下列命题:
①若a、c异号,则方程 ax2+bx+c=0必有两个不相等的实数根;
②若4a-2b+c=0,则方ax2+bx+c=0有两个不等实根;
③若方程ax2+bx+c=0的两根互为相反数,则b=0;
④若b=a+c,则ax2+bx+c=0方程有两个不相等的实数根.
其中正确的为( )
①若a、c异号,则方程 ax2+bx+c=0必有两个不相等的实数根;
②若4a-2b+c=0,则方ax2+bx+c=0有两个不等实根;
③若方程ax2+bx+c=0的两根互为相反数,则b=0;
④若b=a+c,则ax2+bx+c=0方程有两个不相等的实数根.
其中正确的为( )
| A、①③ | B、①②③ |
| C、②③④ | D、①③④ |
考点:根的判别式,命题与定理
专题:计算题
分析:由于a、c异号,则△=b2-4ac>0,于是根据判别式的意义可对①进行判断;由于b=
,计算出△=(
)2-4ac=
≥0,于是根据判别式的意义可对②进行判断;由于方程ax2+bx+c=0的两根互为相反数,根据根与系数的关系对③进行判断;由于b=a+c,则计算出△=(a+c)2-4ac=(a-c)2≥0,于是根据判别式的意义可对④进行判断.
| 4a+c |
| 2 |
| 4a+c |
| 2 |
| (4a-c)2 |
| 4 |
解答:解:若a、c异号,则△=b2-4ac>0,所以方程ax2+bx+c=0必有两个不相等的实数根,所以①正确;若4a-2b+c=0,即b=
,则△=(
)2-4ac=
≥0,所以方程ax2+bx+c=0有两个实数根,所以②错误;若方程ax2+bx+c=0的两根互为相反数,则b=0,所以③正确; 若b=a+c,则△=(a+c)2-4ac=(a-c)2≥0,则ax2+bx+c=0有两个实数根,所以④错误.
故选A.
| 4a+c |
| 2 |
| 4a+c |
| 2 |
| (4a-c)2 |
| 4 |
故选A.
点评:本题考查了根的判别式:利用一元二次方程根的判别式(△=b2-4ac)判断方程的根的情况.一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
相关题目
一元二次方程x2-4x+2=0根的情况是( )
| A、没有实数根 |
| B、只有一个实数根 |
| C、有两个相等的实数根 |
| D、有两个不相等的实数根 |
 如图,在⊙0中,已知∠ABC=20°,∠DCA=30°,则∠DOC的大小为
如图,在⊙0中,已知∠ABC=20°,∠DCA=30°,则∠DOC的大小为 如图是扫雷游戏的示意图.点击中间的按钮,若出现的数字是2,表明数字2周围的8个位置有2颗地雷,现任意点击这8个按钮中的一个,则出现地雷的概率( )
如图是扫雷游戏的示意图.点击中间的按钮,若出现的数字是2,表明数字2周围的8个位置有2颗地雷,现任意点击这8个按钮中的一个,则出现地雷的概率( ) 如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB∥DE,AB=DE,AC=DF.求证:BC=EF.
如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB∥DE,AB=DE,AC=DF.求证:BC=EF. 在奉贤创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
在奉贤创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题: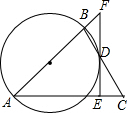 如图,△ABC中,AB=AC,作以AB为直径的⊙O与边BC交于点D,过点D作⊙O的切线,分别交AC、AB的延长线于点E、F.
如图,△ABC中,AB=AC,作以AB为直径的⊙O与边BC交于点D,过点D作⊙O的切线,分别交AC、AB的延长线于点E、F.