题目内容
先化简,再求值:
(1)(1-
)÷
,其中a=-1.
(2)
÷(
-x-2),其中x=
-3.
(1)(1-
| 1 |
| a-1 |
| a2-4a+4 |
| a2-a |
(2)
| 3-x |
| 2x-4 |
| 5 |
| x-2 |
| 3 |
考点:分式的化简求值
专题:
分析:(1)首先将括号里面通分,进而将能因式分解的分子与分母因式分解,即可化简,再利用分式有意的条件得出即可;
(2)首先将括号里面通分,进而将能因式分解的分子与分母因式分解,即可化简,再利用分式有意的条件得出即可.
(2)首先将括号里面通分,进而将能因式分解的分子与分母因式分解,即可化简,再利用分式有意的条件得出即可.
解答:解:(1)(1-
)÷
,
=(
-
)÷
=
×
=
,
当a=-1时,
原式=
=
=
;
(2)
÷(
-x-2),
=
÷[
-
]
=
÷
=
×
=
,
当x=
-3时,原式=
=
=
=
.
| 1 |
| a-1 |
| a2-4a+4 |
| a2-a |
=(
| a-1 |
| a-1 |
| 1 |
| a-1 |
| (a-2)2 |
| a(a-1) |
=
| a-2 |
| a-1 |
| a(a-1) |
| (a-2)2 |
=
| a |
| a-2 |
当a=-1时,
原式=
| a |
| a-2 |
| -1 |
| -1-2 |
| 1 |
| 3 |
(2)
| 3-x |
| 2x-4 |
| 5 |
| x-2 |
=
| 3-x |
| 2(x-2) |
| 5 |
| x-2 |
| (x+2)(x-2) |
| x-2 |
=
| 3-x |
| 2(x-2) |
| 9-x2 |
| x-2 |
=
| 3-x |
| 2(x-2) |
| x-2 |
| (3+x)(3-x) |
=
| 1 |
| 2x+6 |
当x=
| 3 |
| 1 |
| 2x+6 |
| 1 | ||
2(
|
| 1 | ||
2
|
| ||
| 6 |
点评:此题主要考查了分式的化简求值,在分式运算的过程中,要注意对分式的分子、分母进行因式分解,然后简化运算,再运用四则运算法则进行求值计算.分式混合运算的顺序是先乘方,后乘除,最后加减,有括号的先算括号内的,其乘除运算归根到底是乘法运算,实质是约分,分式加减实质是通分,结果要化简.关于化简求值,近年来出现了一种开放型问题,题目中给定几个数字,要考虑分母有意义的条件,不要盲目代入.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
一元二次方程x2-4x+2=0根的情况是( )
| A、没有实数根 |
| B、只有一个实数根 |
| C、有两个相等的实数根 |
| D、有两个不相等的实数根 |
 如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB∥DE,AB=DE,AC=DF.求证:BC=EF.
如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB∥DE,AB=DE,AC=DF.求证:BC=EF.
 在奉贤创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
在奉贤创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
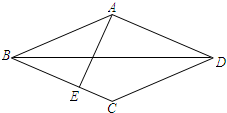 已知:如图,在菱形ABCD中,AE⊥BC,垂足为E,对角线BD=4,tan∠CBD=
已知:如图,在菱形ABCD中,AE⊥BC,垂足为E,对角线BD=4,tan∠CBD=