题目内容
如图，在?ABCD中，E为CD上一点，连接AE、BD，且AE、BD交于点F，S△DEF：S△ABF=4：25，则DE：EC=（ ）
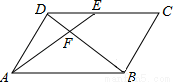
A、2：5 B、2:3 C、3:5 D、3:2
B
【解析】
试题分析：先根据平行四边形的性质及相似三角形的判定定理得出△DEF∽△BAF，再根据
=4：10：25即可得出其相似比，由相似三角形的性质即可求出
的值，由AB=CD即可得出结论DE：EC=2：3．
故选A．
考点：平行四边形的性质,相似三角形的判定定理
练习册系列答案
相关题目
，若△AEF的面积为2，则四边形EBCF的面积为 ．
的图象上有三个点A、B、C，过这三个点分别向x轴、y轴作垂线，过每一点所作的两条垂线段与x轴、y轴围成的矩形的面积分别为
、
、
，则（ ）．
B．
D．
，
，1的卡片，乙同学手中藏有三张分别标有数字1，3，2的卡片，卡片外形相同，现从甲乙两人手中各任取一张卡片，并将它们的数字分别记为
，
．
，
能使得
有两个不相等的实数根，则甲获胜；否则乙获胜．请问这样的游戏规则公平吗？请你用概率知识解释．