题目内容
如图1,在平面直角坐标系中,二次函数y=ax2 -2x+2的图象与y轴交于点C,以OC为一边向左侧作正方形OCBA,点B刚好落在抛物线上.
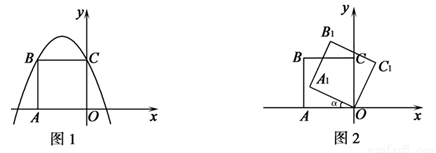
(1)求a的值;
(2)若点D在二次函数y=ax2 -2x+2的图象的对称轴上,点E在二次函数y=ax2 ﹣2x+2的图象上,是否存在以B,C,D,E四点为顶点的四边形为平行四边形?若存在,请直接写出所有满足条件的点E的坐标;若不存在,请说明理由.
(3)如图2,把正方形OCBA绕点O顺时针旋转α后得到正方形A1B1C1O(0°<α<90°)。在旋转过程中,若点A1落在二次函数y=ax2﹣2x+2的图象对称轴上,求出此时的点B1的坐标.
(1)-1;(2)(-1,3)或(-3,-1)或(1,-1),(3)(2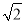 sin15°,2
sin15°,2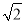 cos15°).
cos15°).
【解析】
试题分析:(1)先求出点C的坐标,再根据正方形的边长相等,得出点B的坐标,代入y=ax2-2x+2,即可得出a的值.
(2)分两种情况求【解析】
①当点E在抛物线顶点时;②当BC∥DE,且DE=BC=2时,即可求出答案;
(3)①由点A1落在二次函数对称轴上,OA1=2,可得出∠A1OA=60°,进而得出∠BOB1=60°,求出∠B1OC=15°,利用三角函数表示点B1的坐标即可;
②设F(-1,m),由△A1B1F∽△HOF得出A1F=2m,由OB1=OB=2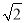 ,得出B1H=
,得出B1H=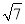 ,在Rt△A1B1F中由勾股定理A1F2+A1B12=B1F2,列出方程(2m)2+22=(
,在Rt△A1B1F中由勾股定理A1F2+A1B12=B1F2,列出方程(2m)2+22=(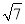 -m)2求出m的值,即可得出点F的坐标.
-m)2求出m的值,即可得出点F的坐标.
试题解析:(1)二次函数y=ax2-2x+2的图象与y轴交于点C,
∴C(0,2),
∵以OC为一边向左侧作正方形OCBA,点B刚好落在抛物线上.
∴B(-2,2),把B(-2,2)代入y=ax2-2x+2,得2=4a+4+2,解得a=-1
(2)①当点E在抛物线顶点时,
∵二次函数的解析式为y=-x2-2x+2.
∴E(-1,3)
∵点D在二次函数的对称轴上,
∴当E(-1,3)以B,C,D,E四点为顶点的四边形为平行四边形
②当BC∥DE,且DE=BC=2时,
∵点D在二次函数的对称轴上,
∴D的横坐标为-1,
∴设点E的横坐标为t,则有-1-t=2,或t-(-1)=2,解得t=-3或1.
∴E(-3,-1)或(1,-1)
综上所述:当点E的坐标为(-1,3)或(-3,-1)或(1,-1),以B,C,D,E四点为顶点的四边形为平行四边形.
(3)如图1,
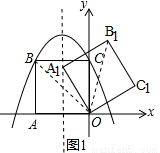
∵点A1落在二次函数对称轴上,OA1=2
∴∠A1OA=60°,
∴∠BOB1=60°,
∴∠B1OC=60°-45°=15°,
∵OB1=OB=2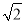 ,
,
∴B1(2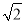 sin15°,2
sin15°,2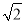 cos15°).
cos15°).
考点:二次函数综合题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案 .
. 是锐角,且
是锐角,且 计算
计算
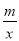 (m≠0)的图象可能是( )
(m≠0)的图象可能是( )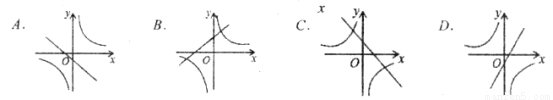
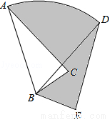

 为⊙
为⊙ 的直径,
的直径, ,且
,且 ,则
,则 .
.