题目内容
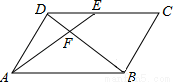
如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连接EF与边CD相交于点G,连接BE与对角线AC相交于点H, AE=CF,BE=EG。

(1)求证:EF//AC;
(2)求∠BEF大小;
(3)求证:
60°
【解析】
试题分析:(1)根据有一组对边平行且相等的四边形是平行四边形即可判定.
(2)先确定△GCF是等腰直角三角形,得出CG=AE,然后通过△BAE≌△BCG,得出BE=BG=EG,即可求得.
(3)因为△BEG是等边三角形,∠ABC=90°,∠ABE=∠CBG,从而求得∠ABE=15°,然后通过求得△AHB∽△FGB,即可求得.
试题解析:(1)证明:
∴四边形AECF是□AECF
∴EF∥AC
(2)连接BG

又∠ACB=45°,∴∠F=∠CGF=45°
CF=CG=AE
AB=BC
∠BAE=∠BCG
 Rt△BAE≌Rt△BCG
Rt△BAE≌Rt△BCG
∴BE=BG
∴BE=BG=EG
∴∠BEF=60°
(3)∠BAC=∠F=45°
由△BAE≌△BCG
∴∠ABE=∠FBG=15°
∴△ABH∽△FBG
∴
考点:平行四边形的性质与判定,等腰三角形性质,全等三角形的性质与判定

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 的值为( )
的值为( )
 B.
B. C.
C. D.
D.