题目内容
15.在平面直角坐标系中,点P为直线y=-x+4上的一个动点,O为坐标原点,则OP的最小值为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | $\sqrt{6}$ | D. | $\sqrt{10}$ |
分析 根据点到直线的最短距离是垂线段的长度,然后根据勾股定理和等腰直角三角形的性质即可解答本题.
解答  解:∵点P为直线y=-x+4上的一个动点,O为坐标原点,
解:∵点P为直线y=-x+4上的一个动点,O为坐标原点,
∴点O(0,0),
作OP⊥直线y=-x+4于点O,直线y=-x+4交x轴于点B,交y轴于点A,如右图所示,
∴点A(0,4),点B的坐标为(4,0),
∴AB=$\sqrt{{4}^{2}+{4}^{2}}=4\sqrt{2}$,
∴OP=$\frac{1}{2}AB=2\sqrt{2}$
即OP的最小值是2$\sqrt{2}$,
故选B.
点评 本题考查一次函数图象上点的坐标特征、垂线段最短,解答本题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
10.下列运算正确的是( )
| A. | $\sqrt{18}$-$\sqrt{8}$=$\sqrt{10}$ | B. | (-3xy)2=6x2y2 | C. | (-21)0=1 | D. | a6÷a2=a3 |
4. 如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中不一定成立的是( )
如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中不一定成立的是( )
 如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中不一定成立的是( )
如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中不一定成立的是( )| A. | S△BEC=2S△CEF | B. | EF=CF | C. | ∠DCF=$\frac{1}{2}$∠BCD | D. | ∠DFE=3∠AEF |
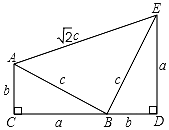 如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=$\sqrt{2}$c,这时我们把关于x的形如ax2+$\sqrt{2}$cx+b=0的一元二次方程称为“勾系一元二次方程”.
如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=$\sqrt{2}$c,这时我们把关于x的形如ax2+$\sqrt{2}$cx+b=0的一元二次方程称为“勾系一元二次方程”.