题目内容
7.二次函数y=x2+(2m-1)x+m2-1的图象与x轴交于点A(x1,0)、B(x2,0),且x12+x22=33,则m的值为( )| A. | 5 | B. | -3 | C. | 5或-3 | D. | 以上都不对 |
分析 二次函数解析式令y=0得到关于x的一元二次方程,利用根与系数关系表示出两根之和与两根之积,已知等式变形后代入求出m的值即可.
解答 解:令y=0,得到x2+(2m-1)x+m2-1=0,
∵二次函数图象与x轴交于点A(x1,0)、B(x2,0),且x12+x22=33,
∴x1+x2=-(2m-1),x1x2=m2-1,△=(2m-1)2-4(m2-1)≥0,
∴(x1+x2)2-2x1x2=(2m-1)2-2(m2-1)=33,
整理得:m2-2m-15=0,即(m-5)(m+3)=0,
解得:m=5或m=-3,
当m=5时,二次函数为y=x2+9x+24,此时△=81-96=-15<0,与x轴没有交点,舍去,
则m的值为-3,
故选B
点评 此题考查了抛物线与x轴的交点,熟练掌握二次函数性质是解本题的关键.

练习册系列答案
相关题目
17.三角形三边长分别为①3,4,5②5,12,13③17,8,15④1,3,2$\sqrt{2}$.其中直角三角形有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.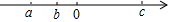 已知有理数a、b、c在数轴上对应的点的位置如图所示,化简$\frac{a}{|a|}$-$\frac{a-c}{|a-c|}$+$\frac{|b|}{b}$的结果为( )
已知有理数a、b、c在数轴上对应的点的位置如图所示,化简$\frac{a}{|a|}$-$\frac{a-c}{|a-c|}$+$\frac{|b|}{b}$的结果为( )
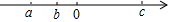 已知有理数a、b、c在数轴上对应的点的位置如图所示,化简$\frac{a}{|a|}$-$\frac{a-c}{|a-c|}$+$\frac{|b|}{b}$的结果为( )
已知有理数a、b、c在数轴上对应的点的位置如图所示,化简$\frac{a}{|a|}$-$\frac{a-c}{|a-c|}$+$\frac{|b|}{b}$的结果为( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
15.下列方程中两个实数根的和等于2的方程是( )
| A. | 2x2-4x+3=0 | B. | 2x2-2x-3=0 | C. | 2y2+4y-3=0 | D. | 2t2-4t-3=0 |
12.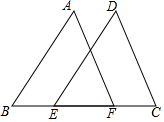 如图,点E,F在BC上,BE=CF,∠B=∠C,若要证明△ABF≌△DCE,则还需要补充的条件不可能是( )
如图,点E,F在BC上,BE=CF,∠B=∠C,若要证明△ABF≌△DCE,则还需要补充的条件不可能是( )
 如图,点E,F在BC上,BE=CF,∠B=∠C,若要证明△ABF≌△DCE,则还需要补充的条件不可能是( )
如图,点E,F在BC上,BE=CF,∠B=∠C,若要证明△ABF≌△DCE,则还需要补充的条件不可能是( )| A. | ∠A=∠D | B. | ∠AFB=∠DEC | C. | AF=DE | D. | AB=CD |
19.将一次函数y=x的图象向上平移2个单位,平移后,若y>0,则x的取值范围是( )
| A. | x>4 | B. | x>-4 | C. | x>2 | D. | x>-2 |
16.单项式-$\frac{2{x}^{3}{y}^{2}z}{3}$的系数是( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |