题目内容
17.三角形三边长分别为①3,4,5②5,12,13③17,8,15④1,3,2$\sqrt{2}$.其中直角三角形有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.
解答 解:①32+42=52,符合勾股定理的逆定理,能构成直角三角形;
②52+122=132,符合勾股定理的逆定理,能构成直角三角形;
③82+152=172,符合勾股定理的逆定理,能构成直角三角形;
④12+(2$\sqrt{2}$)2=32,符合勾股定理的逆定理,能构成直角三角形.
故选:D.
点评 本题考查了勾股定理的逆定理,即如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
相关题目
12.若y=kx-4的函数值y随x的增大而减小,则k的值可能是下列的( )
| A. | -4 | B. | 0 | C. | 1 | D. | 3 |
2.一个整式减去a-b后所得的结果是-a-b,这这个整式是( )
| A. | -2a | B. | -2b | C. | 2a | D. | 2b |
9.已知P1(x1,y1),P2(x2,y2),P3(x3,y3)是反比例函数y=$\frac{2}{x}$的图象上的三点,且x1<x2<0<x3,则y1、y2、y3的大小关系是 ( )
| A. | y3<y2<y1 | B. | y2<y1<y3 | C. | y1<y2<y3 | D. | y2<y3<y1 |
6.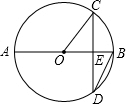 如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,连接OC,DB,若∠CDB=30°,⊙O的半径为4$\sqrt{3}$cm,则弦CD的长为( )
如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,连接OC,DB,若∠CDB=30°,⊙O的半径为4$\sqrt{3}$cm,则弦CD的长为( )
 如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,连接OC,DB,若∠CDB=30°,⊙O的半径为4$\sqrt{3}$cm,则弦CD的长为( )
如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,连接OC,DB,若∠CDB=30°,⊙O的半径为4$\sqrt{3}$cm,则弦CD的长为( )| A. | 8$\sqrt{3}$cm | B. | 12cm | C. | 6$\sqrt{3}$cm | D. | 8cm |
7.二次函数y=x2+(2m-1)x+m2-1的图象与x轴交于点A(x1,0)、B(x2,0),且x12+x22=33,则m的值为( )
| A. | 5 | B. | -3 | C. | 5或-3 | D. | 以上都不对 |
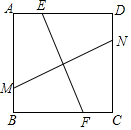 如图,正方形ABCD内有两条相交线段MN、EF,M、N、E、F分别在边AB、CD、AD、BC上.
如图,正方形ABCD内有两条相交线段MN、EF,M、N、E、F分别在边AB、CD、AD、BC上. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①a>0;②b>0;③c<0;b2-4ac>0中,正确的个数有( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①a>0;②b>0;③c<0;b2-4ac>0中,正确的个数有( )