题目内容
19. (1)解方程:4(x+1)2-169=0
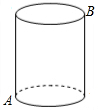
(1)解方程:4(x+1)2-169=0(2)一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是多少?
分析 (1)先求得(x+1)2的值,然后再利用直接开平方法求解即可;
(2)先求得圆柱体的底面周长,然后将侧面展开,然后连接AB,最后利用勾股定理求得AB的长即可.
解答 解:(1)∵4(x+1)2-169=0
∴(x+1)2=$\frac{169}{4}$,
∴x-1=±6.5.
∴x=7.5或x=-5.5.
(2)解:将圆柱体的侧面展开得到如图所示的矩形,连接AB. ∵圆柱的底面半径为2cm
∵圆柱的底面半径为2cm
∴AC=$\frac{1}{2}$×2•π•2=2π.
∵π取3,
∴AC=6cm.
在Rt△ACB中,AB2=AC2+CB2=36+64=100,
AB=10cm.
所以蚂蚁要爬行的最短距离为10cm.
点评 本题主要考查的是平面展开-路径最短问题、解二元一次方程,化曲为直是解答问题(2)的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
10.根据如表回答下列问题:
(1)275.56的平方根是±16.6;
(2)$\sqrt{2.8224}$=1.68;
(3)$\sqrt{270}$在哪两个相邻数之间?为什么?
| x | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 | 16.9 | 17.0 |
| x2 | 262.44 | 265.69 | 268.96 | 272.25 | 275.56 | 278.89 | 282.24 | 285.61 | 289 |
(2)$\sqrt{2.8224}$=1.68;
(3)$\sqrt{270}$在哪两个相邻数之间?为什么?
4.随着人们生活水平的提高,家用轿车越来越多地进入家庭.小明家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如下表),以50km为标准,多于50km的记为“+”,不足50km的记为“-”,刚好50km的记为“0”.
(1)请求出这七天中平均每天行驶多少千米?
(2)若每行驶100km需用汽油6升,汽油价7.22元/升,请估计小明家一个月(按30天计)的汽油费用是多少元?
| 第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
| 路程(km) | -8 | -11 | -14 | 0 | -16 | +41 | +8 |
(2)若每行驶100km需用汽油6升,汽油价7.22元/升,请估计小明家一个月(按30天计)的汽油费用是多少元?
11.若|a|=-a,则a为( )
| A. | 正数 | B. | 0和正数 | C. | 负数 | D. | 0和负数 |
9.y=x2-2x-3的顶点坐标和对称轴( )
| A. | (-1,-4),直线x=-1 | B. | (1,-4),直线x=1 | C. | (-1,4),直线x=-1 | D. | (1,4),直线x=1 |
 在长为10m,宽为8m的长方形空地中,沿平行于长方形各边的方向分割出三个全等的小长方形花圃,其示意图如图所示.则小长方形花圃的长和宽分别是多少?
在长为10m,宽为8m的长方形空地中,沿平行于长方形各边的方向分割出三个全等的小长方形花圃,其示意图如图所示.则小长方形花圃的长和宽分别是多少?