题目内容
8．如图，在边长为2a的正方形中央剪去一边长为（a+2）的小正方形（a＞2），将剩余部分剪开密铺成一个平行四边形，求该平行四边形的面积．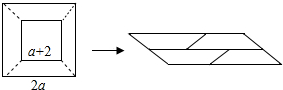
分析 根据拼成的平行四边形的面积等于大正方形的面积减去小正方形的面积，列式整理即可得解．
解答 解：（2a）2-（a+2）2
=4a2-a2-4a-4
=3a2-4a-4．
答：平行四边形的面积为3a2-4a-4．
点评 本题考查了平方差公式的几何背景，根据拼接前后的图形的面积相等列式是解题的关键．
练习册系列答案
相关题目
18．
两个反比例函数y=$\frac{k}{x}$和y=$\frac{1}{x}$在第一象限内的图象如图所示，点P在y=$\frac{k}{x}$的图象上，PC⊥x轴于点C，交y=$\frac{1}{x}$的图象于点A，PD⊥y轴于点D，交y=$\frac{k}{x}$的图象于点B，当点P在y=$\frac{1}{x}$的图象上运动时，下列结论错误的是（ ）
两个反比例函数y=$\frac{k}{x}$和y=$\frac{1}{x}$在第一象限内的图象如图所示，点P在y=$\frac{k}{x}$的图象上，PC⊥x轴于点C，交y=$\frac{1}{x}$的图象于点A，PD⊥y轴于点D，交y=$\frac{k}{x}$的图象于点B，当点P在y=$\frac{1}{x}$的图象上运动时，下列结论错误的是（ ）| A． | △ODB与△OCA的面积相等 | |
| B． | 当点A是PC的中点时，点B一定是PD的中点． | |
| C． | 只有当四边形OCPD为正方形时，四边形PAOB的面积最大 | |
| D． | $\frac{CA}{PA}$=$\frac{DB}{PB}$ |
如图所示，每一个小方格都是边长为1个单位的正方形．△ABC的三个顶点都在格点上，以点O为坐标原点建立平面直角坐标系．
如图，在平面直角坐标系中有Rt△ABC，∠A=90°，AB=AC，A（-2，0）、B（0，1）、C（m，n）．
如图，已知菱形ABCD的边AB长为8，∠ABC=60°．求：
17．若多项式a2+4a+k2是完全平方式，则常数k的值为（ ）
| A． | 2 | B． | 4 | C． | ±4 | D． | ±2 |
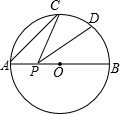如图，AB是⊙O的直径，AB=2，点C是半圆弧AB上的一点，且∠CAB=40°，点D是BC的中点，点P是直径AB上的动点，则线段PC+PD的最小值是$\sqrt{3}$．