题目内容
13.已知菱形的边长为$\sqrt{62}$,其中一条对角线长为4$\sqrt{2}$,则这个菱形的面积为24$\sqrt{3}$.分析 首先根据题意画出图形,然后由菱形的边长为$\sqrt{62}$,其中一条对角线长为4$\sqrt{2}$,求得另一条对角线的长,继而求得答案.
解答  解:如图:∵菱形的边长为$\sqrt{62}$,其中一条对角线长为4$\sqrt{2}$,
解:如图:∵菱形的边长为$\sqrt{62}$,其中一条对角线长为4$\sqrt{2}$,
∴AB=$\sqrt{62}$,OA=$\frac{1}{2}$×4$\sqrt{2}$=2$\sqrt{2}$,AC⊥BD,
∴OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=3$\sqrt{6}$,
∴BD=2OB=6$\sqrt{6}$,
∴这个菱形的面积为:$\frac{1}{2}$AC•BD=$\frac{1}{2}$×4$\sqrt{2}$×6$\sqrt{6}$=24$\sqrt{3}$.
故答案为:24$\sqrt{3}$.
点评 此题考查了菱形的性质以及勾股定理.注意菱形的面积等于其对角线积的一半.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4. 如图,菱形ABCD的对角线BD长为4$\sqrt{3}$cm,高AE长为2$\sqrt{3}$cm,则菱形ABCD的周长为( )
如图,菱形ABCD的对角线BD长为4$\sqrt{3}$cm,高AE长为2$\sqrt{3}$cm,则菱形ABCD的周长为( )
 如图,菱形ABCD的对角线BD长为4$\sqrt{3}$cm,高AE长为2$\sqrt{3}$cm,则菱形ABCD的周长为( )
如图,菱形ABCD的对角线BD长为4$\sqrt{3}$cm,高AE长为2$\sqrt{3}$cm,则菱形ABCD的周长为( )| A. | 20cm | B. | 16cm | C. | 12cm | D. | 8cm |
1.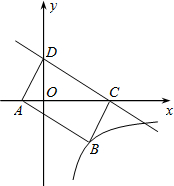 如图,直线y=-$\frac{1}{2}$x+m(m>0)与x轴交于点C,与y轴交于点D,以CD为边作矩形ANCD,点A在x轴上.双曲线y=$-\frac{6}{x}$经过点B,与直线CD交于点E,则点E的坐标为( )
如图,直线y=-$\frac{1}{2}$x+m(m>0)与x轴交于点C,与y轴交于点D,以CD为边作矩形ANCD,点A在x轴上.双曲线y=$-\frac{6}{x}$经过点B,与直线CD交于点E,则点E的坐标为( )
 如图,直线y=-$\frac{1}{2}$x+m(m>0)与x轴交于点C,与y轴交于点D,以CD为边作矩形ANCD,点A在x轴上.双曲线y=$-\frac{6}{x}$经过点B,与直线CD交于点E,则点E的坐标为( )
如图,直线y=-$\frac{1}{2}$x+m(m>0)与x轴交于点C,与y轴交于点D,以CD为边作矩形ANCD,点A在x轴上.双曲线y=$-\frac{6}{x}$经过点B,与直线CD交于点E,则点E的坐标为( )| A. | ($\frac{15}{4}$,-$\frac{8}{5}$) | B. | (4,-$\frac{3}{2}$) | C. | ($\frac{9}{2}$,-$\frac{4}{3}$) | D. | (6,-1) |
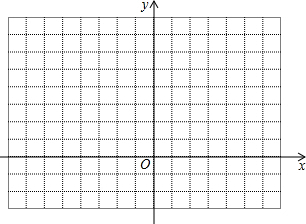 (1)在平面直角坐标系中,描出下列3个点:A (-1,0),B (3,-1),C (4,3);顺次连接A,B,C,组成△ABC.
(1)在平面直角坐标系中,描出下列3个点:A (-1,0),B (3,-1),C (4,3);顺次连接A,B,C,组成△ABC.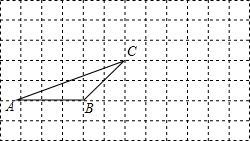 如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格).
如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格).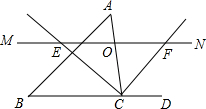 如图,在锐角△ABC中,点O是AC边上的一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,下列结论中正确的是( )
如图,在锐角△ABC中,点O是AC边上的一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,下列结论中正确的是( )