题目内容
4．若$\sqrt{2x-1}$有意义，则x的取值范围是x≥$\frac{1}{2}$；若$\frac{\sqrt{x+1}}{x-1}$有意义，则x的取值范围是x≥-1且x≠1．分析 根据二次根式有意义的条件列出关于x的不等式，求出x的取值范围；再由二次根式及分式有意义的条件列出关于x的不等式组，求出x的取值范围即可．
解答 解：∵$\sqrt{2x-1}$有意义，
∴2x-1≥0，解得x≥$\frac{1}{2}$；
∵$\frac{\sqrt{x+1}}{x-1}$有意义，
∴$\left\{\begin{array}{l}x+1≥0\\ x-1≠0\end{array}\right.$，解得x≥-1且x≠1．
故答案为：x≥$\frac{1}{2}$，x≥-1且x≠1．
点评 本题考查的是二次根式有意义的条件，熟知二次根式具有非负性是解答此题的关键．
练习册系列答案
相关题目
15．
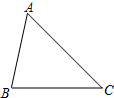在锐角△ABC中，AB=5，BC=6，∠ACB=45°（如图），将△ABC绕点B按逆时针方向旋转得到△A′BC′（顶点A、C分别与A′、C′对应），当点C′在线段CA的延长线上时，则AC′的长度为（ ）
在锐角△ABC中，AB=5，BC=6，∠ACB=45°（如图），将△ABC绕点B按逆时针方向旋转得到△A′BC′（顶点A、C分别与A′、C′对应），当点C′在线段CA的延长线上时，则AC′的长度为（ ）| A． | $\sqrt{2}$+$\sqrt{7}$ | B． | 3$\sqrt{2}$-$\sqrt{7}$ | C． | 3$\sqrt{2}$+$\sqrt{7}$ | D． | 3-$\sqrt{7}$ |
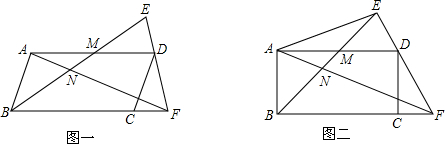
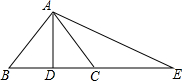如图，AD⊥BC，BD=DC，点C在AE的垂直平分线上．