题目内容
4.已知抛物线y=x2-(m-3)x-m.求证:无论m为何值时,抛物线与x轴总有两个交点.分析 首先确定a、b、c,然后证明△>0即可判断.
解答 证明:a=1,b=-(m-3),c=-m.
△=b2-4ac=(m-3)2+4m
=m2-2m+9
=(m-1)2+8.
∵(m-1)2≥0,8≥0.
则△>0,
∴无论m为何值时,抛物线与x轴总有两个交点.
点评 本题考查了二次函数与x轴的交点,当△>0时,函数与x轴有两个交点;当△=0时,有一个交点,即顶点;当△<0时,没有交点.

练习册系列答案
相关题目
15. 如图,有一个长为15米,宽为10米的长方形草地,在草地中间有一条弯曲的小路,小路的任何地方的宽度都是1米,那么这片草地的绿化面积是( )平方米.
如图,有一个长为15米,宽为10米的长方形草地,在草地中间有一条弯曲的小路,小路的任何地方的宽度都是1米,那么这片草地的绿化面积是( )平方米.
 如图,有一个长为15米,宽为10米的长方形草地,在草地中间有一条弯曲的小路,小路的任何地方的宽度都是1米,那么这片草地的绿化面积是( )平方米.
如图,有一个长为15米,宽为10米的长方形草地,在草地中间有一条弯曲的小路,小路的任何地方的宽度都是1米,那么这片草地的绿化面积是( )平方米.| A. | 150 | B. | 140 | C. | 130 | D. | 120 |
19.七边形的内角和是( )
| A. | 1 260度 | B. | 1 080度 | C. | 900度 | D. | 720度 |
9. 如图,在线段AE上依次有B、C、D三点,则图中共有线段( )
如图,在线段AE上依次有B、C、D三点,则图中共有线段( )
 如图,在线段AE上依次有B、C、D三点,则图中共有线段( )
如图,在线段AE上依次有B、C、D三点,则图中共有线段( )| A. | 1条 | B. | 4条 | C. | 8条 | D. | 10条 |
 如图,四边形OABC和ADEF均为正方形,反比例函数y=$\frac{8}{x}$的图象分别经过AB的中点M及DE的中点N,则正方形ADEF的边长为-2+2$\sqrt{5}$.
如图,四边形OABC和ADEF均为正方形,反比例函数y=$\frac{8}{x}$的图象分别经过AB的中点M及DE的中点N,则正方形ADEF的边长为-2+2$\sqrt{5}$. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论: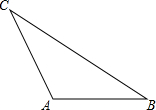 为了美化环境,某小区要在如图所示的三角形空地上作一个半圆形花坛并使之满足以下要求:
为了美化环境,某小区要在如图所示的三角形空地上作一个半圆形花坛并使之满足以下要求: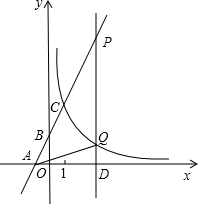 如图,在平面直角坐标系xOy中,直线y=2x+n与x轴、y轴分别交于点A、B,与双曲线y=$\frac{4}{x}$在第一象限内交于点C(1,m).
如图,在平面直角坐标系xOy中,直线y=2x+n与x轴、y轴分别交于点A、B,与双曲线y=$\frac{4}{x}$在第一象限内交于点C(1,m).