题目内容
20.如图,△ABE、△ADF都是等边三角形,BF与ED交点C,(1)如图1,求证BF=ED;
(2)如图2,求证:AC平分∠BCD;
(3)如图3,若∠EAF=30°,连接EF,EF⊥EA于E,连接BD交AF于G,FG=2$\sqrt{5}$,求EF的长.
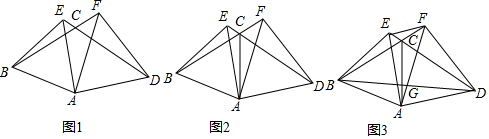
分析 (1)根据等边三角形得:AB=AE,AF=AD,∠BAE=∠DAF=60°,所以∠BAF=∠EAD,根据SAS证明△BAF≌△EAD,则BF=ED;
(2)分别作△BAF和△EAD的高线AM、AN,根据面积法证明AM=AN,所以由角平分线的逆定理得:A在∠BCD的平分线上,即AC平分∠BCD;
(3)作辅助线,构建直角三角形,证明∠BND=90°,得直角△BND,设EF=x,根据30°角的性质和三角函数依次表示:FD=AF=2x,AE=BE=$\sqrt{3}$x,FN=$\frac{1}{2}$x,EN=$\frac{\sqrt{3}}{2}$x,在直角△BND,利用∠BDN的正切列式,求出DM的长,得出AF的长,最后求出EF的长.
解答  证明:(1)如图1,∵△ABE、△ADF都是等边三角形,
证明:(1)如图1,∵△ABE、△ADF都是等边三角形,
∴AB=AE,AF=AD,∠BAE=∠DAF=60°,
∴∠BAE+∠EAF=∠DAF+∠EAF,
即∠BAF=∠EAD,
∴△BAF≌△EAD,
∴BF=ED;
(2)如图2, 过A作AM⊥BF于M,AN⊥DE于N,
过A作AM⊥BF于M,AN⊥DE于N,
∵△BAF≌△EAD,
∴S△BAF=S△EAD,
∴$\frac{1}{2}$BF•AM=$\frac{1}{2}$DE•AN,
∵BF=DE,
∴AM=AN,
∴A在∠BCD的平分线上,即AC平分∠BCD;
(3)如图3,延长BE、DF交于N,过G作GM⊥DF于M,
∵△AFD是等边三角形,
∴∠GFM=60°,
在Rt△GFM中,sin∠GFM=$\frac{GM}{GF}$,
sin60°=$\frac{GM}{2\sqrt{5}}$,
GM=$\frac{\sqrt{3}}{2}$×2$\sqrt{5}$=$\sqrt{15}$,
∵∠BAE=∠FAD=60°,∠EAF=30°,
∴∠EAD=60°+60°+30°=150°,
∴∠ABD+∠ADB=180°-150°=30°,
∵∠EBA+∠FDA=60°+60°=120°,
∴∠EBD+∠FDB=120°-30°=90°,
∴∠BND=90°,
在Rt△AEF中,∠EAF=30°,
∴∠EFA=60°,
∴∠EFN=180°-∠AFD-∠EFA=60°,
∴∠NEF=30°,
设EF=x,则FD=AF=2x,AE=BE=$\sqrt{3}$x,FN=$\frac{1}{2}$x,EN=$\frac{\sqrt{3}}{2}$x,
Rt△BND中,tan∠BDN=$\frac{BN}{ND}=\frac{GM}{DM}$,
∴$\frac{\sqrt{3}x+\frac{\sqrt{3}}{2}x}{\frac{1}{2}x+2x}$=$\frac{\sqrt{15}}{DM}$,
∴DM=$\frac{5\sqrt{5}}{3}$,
∴DF=AF=FM+DM=$\sqrt{5}$+$\frac{5\sqrt{5}}{3}$=$\frac{8\sqrt{5}}{3}$,
∴EF=$\frac{1}{2}$AF=$\frac{4\sqrt{5}}{3}$.
点评 本题是三角形的综合题,比较复杂,考查了等边三角形、直角三角形、全等三角形和特殊三角函数的性质;相对比,(1)和(2)难度适中,(3)比较复杂,第(3)巧妙构建直角△FGM和△BDN是关键;从已知FG入手,根据30°和60°的函数值依次求出各边长,得出最后的结论.

 阅读快车系列答案
阅读快车系列答案| A. | 单项式$\frac{3x{y}^{2}}{5}$的系数是3,次数是2 | B. | 单项式-15ab的系数是15,次数是2 | ||
| C. | $\frac{xy-1}{2}$是二次多项式 | D. | 多项式4x2-3的常数项是3 |
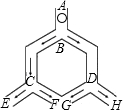 如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达H点的概率是( )
如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达H点的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
 请画出如图所示的几何体从正面、左面、上面三个方向看到的图形.
请画出如图所示的几何体从正面、左面、上面三个方向看到的图形.